
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且(c﹣2a) ![]() =c
=c ![]()
![]()
(1)求B的大小;
(2)已知f(x)=cosx(asinx﹣2cosx)+1,若对任意的x∈R,都有f(x)≤f(B),求函数f(x)的单调递减区间.
【答案】
(1)解:∵(c﹣2a) ![]() =c
=c ![]()
![]() ,即(c﹣2a)accos(π﹣B)=abccosC,
,即(c﹣2a)accos(π﹣B)=abccosC,
∴2accosB=bcosC+ccosB,∴2sinAcosB=sinBcosC+sinCcosB,
∴2sinAcosB=sin(B+C)=sinA,
∴cosB= ![]() ,∴B=
,∴B= ![]()
(2)解:f(x)=cosx(asinx﹣2cosx)+1= ![]() sin2x﹣cos2x=
sin2x﹣cos2x= ![]() sin(2x﹣φ),
sin(2x﹣φ),
∵对任意的x∈R,都有f(x)≤f(B)=f( ![]() ),
),
∴sin( ![]() ﹣φ)=1,∴φ=
﹣φ)=1,∴φ= ![]() ,
,
∴f(x)= ![]() sin(2x﹣
sin(2x﹣ ![]() ),
),
令 ![]() ,解得
,解得 ![]() ≤x≤
≤x≤ ![]() +kπ,k∈Z.
+kπ,k∈Z.
∴函数f(x)的单调递减区间是[ ![]() ,
, ![]() +kπ],k∈Z.
+kπ],k∈Z.
【解析】(1)根据向量的数量积定义和三角恒等变换化简即可求出cosB,得出B的值;(2)化简f(x)的解析式,根据f(B)为f(x)的最大值求出f(x)的解析式,利用正弦函数的单调区间列不等式解出.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某水产养殖户制作一体积为![]() 立方米的养殖网箱(无盖),网箱内部被隔成体积相等的三块长方体区域(如图),网箱.上底面的一边长为
立方米的养殖网箱(无盖),网箱内部被隔成体积相等的三块长方体区域(如图),网箱.上底面的一边长为![]() 米,网箱的四周与隔栏的制作价格是
米,网箱的四周与隔栏的制作价格是![]() 元/平方米,网箱底部的制作价格为
元/平方米,网箱底部的制作价格为![]() 元/平方米.设网箱上底面的另一边长为
元/平方米.设网箱上底面的另一边长为![]() 米,网箱的制作总费用为
米,网箱的制作总费用为![]() 元.
元.
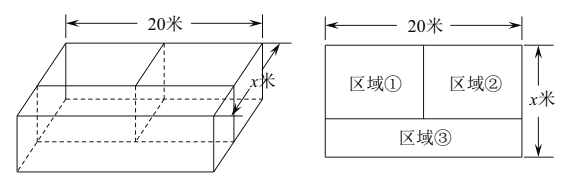
(1)求出![]() 与
与![]() 之间的函数关系,并指出定义域;
之间的函数关系,并指出定义域;
(2)当网箱上底面的另一边长![]() 为多少米时,制作网箱的总费用最少.
为多少米时,制作网箱的总费用最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1的方程为3x+4y﹣12=0.
(1)若直线l2与l1平行,且过点(﹣1,3),求直线l2的方程;
(2)若直线l2与l1垂直,且l2与两坐标轴围成的三角形面积为4,求直线l2的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com