
【题目】如图,在三棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() 为棱
为棱![]() 上的一点,且
上的一点,且![]() 平面
平面![]() .
.
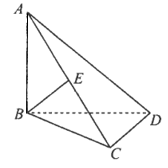
(1)证明:![]() ;
;
(2)设![]() .
.![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .求二面角
.求二面角![]() 的大小.
的大小.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】2020年,新型冠状病毒引发的疫情牵动着亿万人的心,八方驰援战疫情,众志成城克时难,社会各界支援湖北共抗新型冠状病毒肺炎,重庆某医院派出3名医生,2名护士支援湖北,现从这5人中任选2人定点支援湖北某医院,则恰有1名医生和1名护士被选中的概率为( )
A.0.7B.0.4C.0.6D.0.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以直角坐标系的原点
为参数),在以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】美团外卖和百度外卖两家公司其“骑手”的日工资方案如下:美团外卖规定底薪70元,每单抽成1元;百度外卖规定底薪100元,每日前45单无抽成,超出45单的部分每单抽成6元,假设同一公司的“骑手”一日送餐单数相同,现从两家公司个随机抽取一名“骑手”并记录其100天的送餐单数,得到如下条形图:
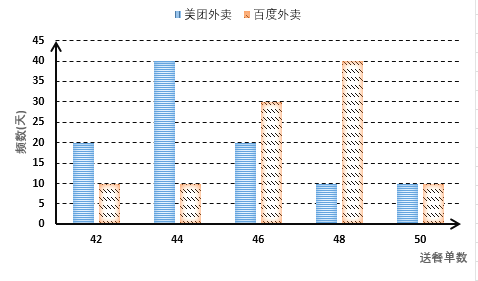
(Ⅰ)求百度外卖公司的“骑手”一日工资![]() (单位:元)与送餐单数
(单位:元)与送餐单数![]() 的函数关系;
的函数关系;
(Ⅱ)若将频率视为概率,回答下列问题:
①记百度外卖的“骑手”日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②小明拟到这两家公司中的一家应聘“骑手”的工作,如果仅从日收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
⑴求椭圆![]() 的标准方程;
的标准方程;
⑵已知动直线![]() 过点
过点![]() 且与椭圆
且与椭圆![]() 交于
交于![]() 两点.试问
两点.试问![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知离心率为![]() 的椭圆
的椭圆![]() 的左顶点为
的左顶点为![]() ,左焦点为
,左焦点为![]() ,及点
,及点![]() ,且
,且![]() 、
、![]() 、
、![]() 成等比数列.
成等比数列.
(1)求椭圆![]() 的方程;
的方程;
(2)斜率不为![]() 的动直线
的动直线![]() 过点
过点![]() 且与椭圆
且与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,记
两点,记![]() ,线段
,线段![]() 上的点
上的点![]() 满足
满足![]() ,试求
,试求![]() (
(![]() 为坐标原点)面积的取值范围.
为坐标原点)面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在新型冠状病毒疫情期间,商业活动受到很大影响某小型零售连锁店总部统计了本地区50家加盟店2月份的零售情况,统计数据如图所示.据估计,平均销售收入比去年同期下降40%,则去年2月份这50家加盟店的平均销售收入约为( )
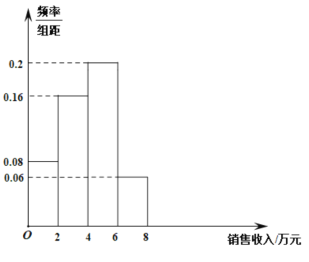
A.6.6万元B.3.96万元C.9.9万元D.7.92万元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com