练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列说法：

    ①将一组数据中的每个数据都加上或减去同一个常数后，方差恒不变；

    ②设有一个回归方程，变量增加一个单位时，平均增加个单位；

    ③线性回归方程必过)；

    ④在一个列联表中，由计算得，则有以上的把握认为这两个变量间有关系．

    其中错误的个数是(　　)

    A. B. C. D.

    【答案】B

    【解析】一组数据都加上或减去同一个常数，数据的平均数有变化，方差不变(方差是反映数据的波动程度的量)，①正确；回归方程中的系数具备直线斜率的功能，对于回归方程 ，当增加一个单位时，平均减少个单位，②错误；由线性回归方程的定义知，线性回归方程= 必过点，③正确；因为，故有以上的把握认为这两个变量间有关系，④正确，即错误的个数为，故选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥中，底面为梯形， 底面， ， ， ， ．　

    （1）求证：平面 平面；

    （2）设为上的一点，满足，若直线与平面所成角的正切值为，求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法： ①一组数据不可能有两个众数；
    ②一组数据的方差必为正数，且方差越大，数据的离散程度越大；
    ③将一组数据中的每个数都加上同一个常数后，方差恒不变；
    ④在频率分布直方图中，每个长方形的面积等于相应小组的频率．
    其中错误的个数有（ ）
    A.0
    B.1
    C.2
    D.3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某城市随机抽取一年（365天）内100天的空气质量指数API的监测数据，结果统计如表：

    API

    [0，50]

    （50，100]

    （100，150]

    （150，200]

    （200，250]

    （250，300]

    ＞300

    空气质量

    优

    良

    轻微污染

    轻度污染

    中度污染

    中度重污染

    重度污染

    天数

    4

    13

    18

    30

    9

    11

    15


    （1）若某企业每天由空气污染造成的经济损失S（单位：元）与空气质量指数API（记为ω）的关系式为： S= 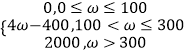，试估计在本年内随机抽取一天，该天经济损失S大于200元且不超过600元的概率；
    （2）若本次抽取的样本数据有30天是在供暖季，其中有8天为重度污染，完成下面2×2列联表，并判断能否有95%的把握认为该市本年空气重度污染与供暖有关？ 附：

    P（K2≥k0）

    0.25

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    k0

    1.323

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    k2=

    非重度污染

    重度污染

    合计

    供暖季

    非供暖季

    合计

    100

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，内角A、B、C所对的边分别是a、b、c，且a+b+c=8．
    （1）若a=2，b= ，求cosC的值；
    （2）若sinAcos2 +sinBcos2 =2sinC，且△ABC的面积S= sinC，求a和b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校高三某班的一次测试成绩的频率分布表以及频率分布直方图中的部分数据如下，请根据此解答如下问题：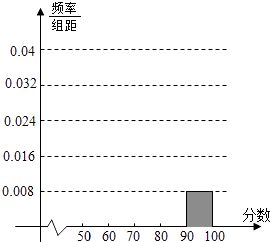

    （1）求班级的总人数；
    （2）将频率分布表及频率分布直方图的空余位置补充完整；
    （3）若要从分数在[80，100）之间的试卷中任取两份分析学生失分情况，在抽取的试卷中，求至少有一份分数在[90，100）之间的概率．

    分组

    频数

    频率

    [50，60）

    0.08

    [60，70）

    7

    [70，80）

    10

    [80，90）

    [90，100）

    2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某电影院共有1000个座位，票价不分等次，根据影院的经营经验，当每张票价不超过10元时，票可全售出；当每张票价高于10元时，每提高1元，将有30张票不能售出，为了获得更好的收益，需给影院定一个合适的票价，需符合的基本条件是：①为了方便找零和算账，票价定为1元的整数倍；②电影院放一场电影的成本费用支出为5750元，票房的收入必须高于成本支出，用x（元）表示每张票价，用y（元）表示该影院放映一场的净收入（除去成本费用支出后的收入） 问：
    （1）把y表示为x的函数，并求其定义域；
    （2）试问在符合基本条件的前提下，票价定为多少时，放映一场的净收人最多？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，已知曲线（为参数），在以原点为极点， 轴的非负半轴为极轴建立的机坐标系中，直线的极坐标方程为.

    （1）求曲线的普通方程和直线的直角坐标方程；

    （2）过点且与直线平行的直线交于两点，求点到两点的距离之积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数y=Asin（ωx+φ）在一个周期内的图象如图，此函数的解析式为（ ）
    A.y=2sin（2x+ ）
    B.y=2sin（2x+ ）
    C.y=2sin（ ﹣ ）
    D.y=2sin（2x﹣ ）

    查看答案和解析>>

    同步练习册答案