
����Ŀ��ij�ͻ�������һ�������ľ�ˮ����ʹ������Ϊʮ�꣬�Ŀˮ��Ϊ�������ˣ�ÿһ�����˶��ɺ��IJ�����о��ʵ��.��ʹ�ù����У�һ����о��Ҫ�����ڸ���������ÿ����![]() ��һ����о����Ҫ����
��һ����о����Ҫ����![]() ��������о��������о�������.����һ����оÿ��
��������о��������о�������.����һ����оÿ��![]() Ԫ��������оÿ��
Ԫ��������оÿ��![]() Ԫ.��һ̨��ˮ����ʹ��������Ҫ�����Ķ�����о�ĸ������ɵļ���Ϊ
Ԫ.��һ̨��ˮ����ʹ��������Ҫ�����Ķ�����о�ĸ������ɵļ���Ϊ![]() .��ͼ�Ǹ���
.��ͼ�Ǹ���![]() ̨�ÿˮ����ʮ��ʹ�����ڸ�����һ����о�ĸ����Ƴɵ���״ͼ.
̨�ÿˮ����ʮ��ʹ�����ڸ�����һ����о�ĸ����Ƴɵ���״ͼ.
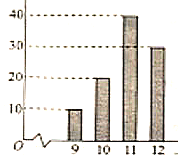
��1�����ͼ��д������![]() ��
��
��2������������Ϣ�����һ̨��ˮ����ʹ�����ڸ���������о�ķ��ô���![]() Ԫ�ĸ��ʣ���
Ԫ�ĸ��ʣ���![]() ̨��ˮ������������о��Ƶ�ʴ���
̨��ˮ������������о��Ƶ�ʴ���![]() ̨��ˮ������������о�����ĸ��ʣ���
̨��ˮ������������о�����ĸ��ʣ���
��3�����ڹ���ˮ����ͬʱ������о������о������![]() ���Żݣ�ʹ�ù����������ٹ������Żݣ�.��������
���Żݣ�ʹ�ù����������ٹ������Żݣ�.��������![]() ̨��ˮ���ڹ�����ͬʱ��ÿ̨������
̨��ˮ���ڹ�����ͬʱ��ÿ̨������![]() ��һ����о��
��һ����о��![]() ��������о��Ϊ������о������
��������о��Ϊ������о������![]() ��
��![]() ����������
����������![]() ̨��ˮ����ʹ�����ڹ�����о�����ܷ��õ�ƽ����.���Դ���Ϊ�������ݣ�����ͻ�����ˮ����ͬʱ��������о������ҲΪ
̨��ˮ����ʹ�����ڹ�����о�����ܷ��õ�ƽ����.���Դ���Ϊ�������ݣ�����ͻ�����ˮ����ͬʱ��������о������ҲΪ![]() ����������һ����о�Ͷ�����о�ĸ���Ӧ�ֱ��Ƕ��٣�
����������һ����о�Ͷ�����о�ĸ���Ӧ�ֱ��Ƕ��٣�
���𰸡���1��![]() ����2��0.3����3��������.
����2��0.3����3��������.
��������
��1������ֱ��ͼ��һ����о�Ͷ�����о֮��Ĺ�ϵ���ɵô𰸣�
��2������������о�ķ��ô���![]() Ԫ��������4��������о��ת��Ϊ����12��һ����о����ֱ��ͼ�ó��𰸣�
Ԫ��������4��������о��ת��Ϊ����12��һ����о����ֱ��ͼ�ó��𰸣�
��3��![]() ��
��![]() �����Է�Ϊ
�����Է�Ϊ![]() ��
��![]() ����������ֱ������ƽ�������õ�����
����������ֱ������ƽ�������õ�����
��1���������֪��һ����о����![]() ��
��![]() ��
��![]() ��ʱ��������о��Ҫ����
��ʱ��������о��Ҫ����![]() ����
����
��һ����о����![]() ��ʱ��������о��Ҫ����
��ʱ��������о��Ҫ����![]() ��������
��������![]() ��
��
��2���������֪������о����![]() ������
������![]() Ԫ��������о����
Ԫ��������о����![]() ������
������![]() Ԫ��
Ԫ��
��![]() ̨��ˮ���У�������о��Ҫ����
̨��ˮ���У�������о��Ҫ����![]() ���ľ�ˮ����
���ľ�ˮ����![]() ̨��������о��Ҫ����
̨��������о��Ҫ����![]() ���ľ�ˮ����
���ľ�ˮ����![]() ̨��
̨��
�衰һ̨��ˮ����ʹ�����ڸ���������о�ķ��ô���![]() Ԫ��Ϊ�¼�
Ԫ��Ϊ�¼�![]() ������
������![]() ��
��
��3����Ϊ![]() ��
��![]() ��
��
��i����![]() ��
��![]() ��
��
����![]() ̨��ˮ���ڸ�����о��������õ�ƽ����Ϊ
̨��ˮ���ڸ�����о��������õ�ƽ����Ϊ
![]()
��ii����![]() ��
��![]() ��
��
����![]() ̨��ˮ���ڸ�����о��������õ�ƽ����Ϊ
̨��ˮ���ڸ�����о��������õ�ƽ����Ϊ
![]()
��������ͻ�����ˮ����ͬʱ��������о������Ϊ![]() ����
����
�ͻ�Ӧ�ù���һ����о![]() ����������о
����������о![]() ����
����


 ����ѧ���ʱѧ����ϵ�д�
����ѧ���ʱѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �Ǻ���y��f��x���ĵ�����������
�Ǻ���y��f��x���ĵ�����������![]() Ϊ
Ϊ![]() �ĵ�������������
�ĵ�������������![]() ��0��ʵ����x0����Ƶ㣨x0��f��x0����Ϊ����y��f��x���Ĺյ㣬���о����֣����е����κ���f��x����ax3+bx2+cx+d��a��0�����йյ㣬�Ҷ��жԳ����ģ���յ���ǶԳ����ģ���f��x����x3��3x2��3x+6����f��
��0��ʵ����x0����Ƶ㣨x0��f��x0����Ϊ����y��f��x���Ĺյ㣬���о����֣����е����κ���f��x����ax3+bx2+cx+d��a��0�����йյ㣬�Ҷ��жԳ����ģ���յ���ǶԳ����ģ���f��x����x3��3x2��3x+6����f��![]() ��+f��
��+f��![]() ��+����+f��
��+����+f��![]() ����_____��
����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij�β����У�ij��40�������ijɼ�����100��ͳ����ͼ��ʾ.
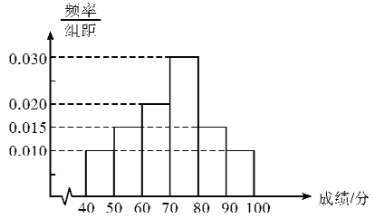
��������40��ѧ���IJ���ɼ�����λ��![]() ��ȷ��0.1��
��ȷ��0.1��
����80������Ϊ���㣬80�ּ�����Ϊ�ϸ��Ƶ�ʷֲ�ֱ��ͼ����±������ж��Ƿ���95%�İ�����Ϊ��ѧ����ɼ����Ա��йأ�
�ϸ� | ���� | �ϼ� | |
���� | 16 | ||
�� | 4 | ||
�ϼ� | 40 |
����
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ���ڣ���һ��ͼ����һ�㰴ij������ת��һ���Ƕȣ��������˶�����ͼ�ε���ת����ͼ��С¬����ͼ�ε���ת���ij�λ�Ļձ꣬�����߳�Ϊa����������ABC ��������O��ʱ����ת��������A1B1C1����![]() .˳������A��A1��B��B1��C��C1��A���õ������λձ�AA1BB1CC1 .
.˳������A��A1��B��B1��C��C1��A���õ������λձ�AA1BB1CC1 .
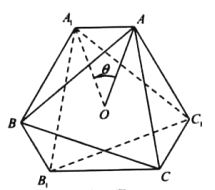
(1)����![]() ʱ���������λձ�������
ʱ���������λձ�������
(2)�������λձ���ܳ������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
![]() ��
��
��1������![]() �ĵ������䣻
�ĵ������䣻
��2��������![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() �������ߵ�б��Ϊ1���ʣ�
�������ߵ�б��Ϊ1���ʣ�![]() ��ʲô��Χȡֵʱ�����������
��ʲô��Χȡֵʱ�����������![]() ������
������![]() ������
������![]() ���ܴ��ڼ�ֵ��
���ܴ��ڼ�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() �Ķ�����Ϊ
�Ķ�����Ϊ![]() ,������һ�κ���
,������һ�κ���![]() ,ʹ�ö��������
,ʹ�ö��������![]() ,����
,����![]() �����,��ƺ���
�����,��ƺ���![]() ��
��![]() �ϵ�����������.���н�����ȷ����__________.(д��������ȷ��������)
�ϵ�����������.���н�����ȷ����__________.(д��������ȷ��������)
��![]() ��
��![]() ��
��![]() �ϵ�����������;
�ϵ�����������;
��![]() ��
��![]() ��
��![]() �ϵ�����������;
�ϵ�����������;
��![]() ��
��![]() ��
��![]() �ϵ�����������;
�ϵ�����������;
��![]() ��
��![]() ��
��![]() �ϵ�����������.
�ϵ�����������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() ��ȡ��������
��ȡ��������![]() ��
��![]() ����ȡ��������
����ȡ��������![]() ��
��![]() ����
����![]() .
.
(1)��ֱ��![]() ��
��![]() �Ľ���
�Ľ���![]() �Ĺ켣
�Ĺ켣![]() �ķ��̣�
�ķ��̣�
(2)��![]() ��ֱ����켣
��ֱ����켣![]() ����
����![]() ���㣬����
���㣬����![]() ��
��![]() ������켣
������켣![]() ������һ��
������һ��![]() ��
��![]() Ϊ�켣
Ϊ�켣![]() ���ҽ��㣬��
���ҽ��㣬��![]() ����֤��
����֤��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1������![]() ��ֵ��ĸ�����
��ֵ��ĸ�����
��2����![]() ��������ֵ��
��������ֵ��![]() ��
��![]() ����
����![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com