
【题目】如图是正方体的平面展开图,在这个正方体中, ①BM与ED平行;
②CN与BE是异面直线;
③CN与BM成60°角;
④DM与BN垂直.
以上四个命题中,正确命题的序号是( )
A.③
B.③④
C.①③
D.①③④
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
【题目】下列4个命题,其中正确的命题是 ①“ ![]() ”是“
”是“ ![]() 不共线”的充要条件;
不共线”的充要条件;
②已知向量 ![]() 是空间两个向量,若
是空间两个向量,若 ![]() ,则向量
,则向量 ![]() 的夹角为60°;
的夹角为60°;
③抛物线y=﹣x2上的点到直线4x+3y﹣8=0的距离的最小值是 ![]() ;
;
④与两圆A:(x+5)2+y2=49和圆B:(x﹣5)2+y2=1都外切的圆的圆心P的轨迹方程为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差为2,前n项和为Sn , 且S1、S2、S4成等比数列.
(1)求数列{an}的通项公式;
(2)令bn=(﹣1)n﹣1 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的右焦点到直线
的右焦点到直线 ![]() 的距离为
的距离为 ![]() ,离心率
,离心率 ![]() ,A,B是椭圆上的两动点,动点P满足
,A,B是椭圆上的两动点,动点P满足 ![]() ,(其中λ为常数).
,(其中λ为常数). 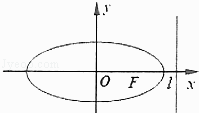
(1)求椭圆标准方程;
(2)当λ=1且直线AB与OP斜率均存在时,求|kAB|+|kOP|的最小值;
(3)若G是线段AB的中点,且kOAkOB=kOGkAB , 问是否存在常数λ和平面内两定点M,N,使得动点P满足PM+PN=18,若存在,求出λ的值和定点M,N;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() ,左焦点
,左焦点 ![]() ,且离心率
,且离心率 ![]() (Ⅰ)求椭圆C的方程;
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l:y=kx+m(k≠0)与椭圆C交于不同的两点M,N(M,N不是左、右顶点),且以MN为直径的圆经过椭圆C的右顶点A.求证:直线l过定点,并求出定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于实数x的不等式﹣x2+bx+c<0的解集是{x|x<﹣3或x>2},则关于x的不等式cx2﹣bx﹣1>0的解集是( )
A.(﹣ ![]() ,
, ![]() )
)
B.(﹣2,3)
C.(﹣∞,﹣ ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
D.(﹣∞,﹣2)∪(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某实验室一天的温度(单位:℃)随时间t(单位:h)的变化近似满足函数关系: f(t)=10﹣ ![]() ,t∈[0,24)
,t∈[0,24)
(Ⅰ)求实验室这一天的最大温差;
(Ⅱ)若要求实验室温度不高于11℃,则在哪段时间实验室需要降温?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com