
【题目】如图,已知四棱锥![]() 的底面为直角梯形,平面
的底面为直角梯形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() 的中点分别是
的中点分别是![]() ,
,![]() .
.
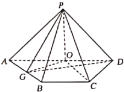
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求点![]() 到平面
到平面![]() 的距离.
的距离.
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点
,点![]() 在
在![]() 轴负半轴上,以
轴负半轴上,以![]() 为边做菱形
为边做菱形![]() ,且菱形
,且菱形![]() 对角线的交点在
对角线的交点在![]() 轴上,设点
轴上,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() ,其中
,其中![]() ,作曲线
,作曲线![]() 的切线,设切点为
的切线,设切点为![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,角A,B,C所对应的分别为a,b,c,且(a+b)(sinA﹣sinB)=(c﹣b)sinC,若a=2,则△ABC的面积的最大值是( )
A.1B.![]() C.2D.2
C.2D.2![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为评估设备![]() 生产某种零件的性能,从设备
生产某种零件的性能,从设备![]() 生产该零件的流水线上随机抽取100个零件为样本,测量其直径后,整理得到下表:
生产该零件的流水线上随机抽取100个零件为样本,测量其直径后,整理得到下表:
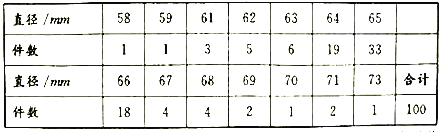
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(I)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进行判定(
,并根据以下不等式进行判定(![]() 表示相应事件的概率):
表示相应事件的概率):
①![]() ;
;
②![]() ;
;
③![]() .
.
判定规则为:若同时满足上述三个式子,则设备等级为甲;若仅满足其中两个,则等级为乙,若仅满足其中一个,则等级为丙;若全部都不满足,则等级为了.试判断设备![]() 的性能等级.
的性能等级.
(Ⅱ)将直径尺寸在![]() 之外的零件认定为是“次品”.
之外的零件认定为是“次品”.
①从设备![]() 的生产流水线上随机抽取2个零件,求其中次品个数
的生产流水线上随机抽取2个零件,求其中次品个数![]() 的数学期望
的数学期望![]() ;
;
②从样本中随意抽取2个零件,求其中次品个数![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分,(1)小问7分,(2)小问5分)
设函数![]()
(1)若![]() 在
在![]() 处取得极值,确定
处取得极值,确定![]() 的值,并求此时曲线
的值,并求此时曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 在
在![]() 上为减函数,求
上为减函数,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分,(1)小问7分,(2)小问5分)
设函数![]()
(1)若![]() 在
在![]() 处取得极值,确定
处取得极值,确定![]() 的值,并求此时曲线
的值,并求此时曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 在
在![]() 上为减函数,求
上为减函数,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研小组为了研究一种治疗新冠肺炎患者的新药的效果,选50名患者服药一段时间后,记录了这些患者的生理指标![]() 和
和![]() 的数据,并统计得到如下的
的数据,并统计得到如下的![]() 列联表(不完整):
列联表(不完整):
|
| 合计 | |
| 12 | 36 | |
| 7 | ||
合计 |
其中在生理指标![]() 的人中,设
的人中,设![]() 组为生理指标
组为生理指标![]() 的人,
的人,![]() 组为生理指标
组为生理指标![]() 的人,他们服用这种药物后的康复时间(单位:天)记录如下:
的人,他们服用这种药物后的康复时间(单位:天)记录如下:
![]() 组:10,11,12,13,14,15,16
组:10,11,12,13,14,15,16
![]() 组:12,13,15,16,17,14,25
组:12,13,15,16,17,14,25
(Ⅰ)填写上表,并判断是否有95%的把握认为患者的两项生理指标![]() 和
和![]() 有关系;
有关系;
(Ⅱ)从![]() ,
,![]() 两组随机各选1人,
两组随机各选1人,![]() 组选出的人记为甲,
组选出的人记为甲,![]() 组选出的人记为乙,求甲的康复时间比乙的康复时间长的概率.
组选出的人记为乙,求甲的康复时间比乙的康复时间长的概率.
附: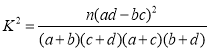 ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com