练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    正三棱柱ABC－A1B1C1的所有棱长均为2，P是侧棱AA1上任意一点．

    (Ⅰ)求证：直线B1P不可能与平面ACC1A1垂直；

    (Ⅱ)当BC1⊥B1P时，求二面角C－B1P－C1的余弦值．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图所示，正三棱柱ABC-A1B1C1的底面边长是2，侧棱长是
    		3
    ，D是AC的中点．
    （1）求证：B1C∥平面A1BD；
    （2）求三棱锥A1-ABD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，正三棱柱ABC-A1B1C1中，D为线段A1C1中点．
    （Ⅰ）求证：BC1∥平面AB1D；
    （Ⅱ）若AA1=
    		3
    ，二面角A-B1D-A1的大小为600，求线段 AB 的长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    【注意：本题的要求是，参照标①的写法，在标号②、③、④、⑤的横线上填写适当步骤，完成(Ⅰ)证明的全过程；并解答(Ⅱ)．】

    如图：在正三棱柱ABC－A1 B1 C1中，AB==a，E，F分别是BB1，CC1上的点且BE=a，CF=2a．

    (Ⅰ)求证：面AEF⊥面ACF；

    (Ⅱ)求三棱锥A1－AEF的体积．

    (Ⅰ)证明：

    ①∵ BE=a，CF=2a，BE∥CF，延长FE与CB延长线交于D，连结AD．

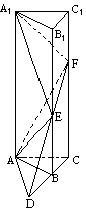
    ∴ △DBE∽△DCF

    ∴

    ②_____________________

    ∴ DB=AB．

    ③______________________

    ∴ DA⊥AC

    ④_______________________

    ∴ FA⊥AD

    ⑤_________________________

    ∴ 面AEF⊥面ACF．

     

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：044

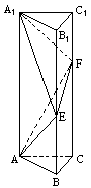
    【注意：本题的要求是，参照标①的写法，在标号②、③、④、⑤的横线上填写适当步骤，完成(Ⅰ)证明的全过程；并解答(Ⅱ)．】

    如图：在正三棱柱ABC－A1 B1 C1中，AB==a，E，F分别是BB1，CC1上的点且BE=a，CF=2a．

    (Ⅰ)求证：面AEF⊥面ACF；

    (Ⅱ)求三棱锥A1－AEF的体积．

    (Ⅰ)证明：

    ①∵ BE=a，CF=2a，BE∥CF，延长FE与CB延长线交于D，连结AD．

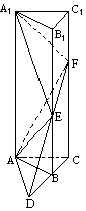
    ∴ △DBE∽△DCF

    ∴

    ②_____________________

    ∴ DB=AB．

    ③______________________

    ∴ DA⊥AC

    ④_______________________

    ∴ FA⊥AD

    ⑤_________________________

    ∴ 面AEF⊥面ACF．

     

    查看答案和解析>>

    科目：高中数学 来源：2009年高考数学文科(湖南卷) 题型：044

    如图3，在正三棱柱ABC－A1，B1，C1中，AB＝4，AA1＝，点D是BC的中点，点E在AC上，且DE⊥A1E

    (Ⅰ)证明：平面A1DE⊥平面ACC1A1；

    (Ⅱ)求直线AD和平面A1DE所成角的正弦值

    查看答案和解析>>

    同步练习册答案