
【题目】已知椭圆![]() (a>b>0)过点(0,
(a>b>0)过点(0,![]() ),且离心率为
),且离心率为![]() 。
。
(Ⅰ)求椭圆E的方程;
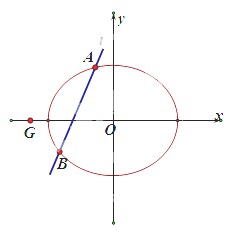
(II)设直线x my 1,(m R)交椭圆E与A,B两点,判断点G(-![]() ,0)与以线段AB为直径的圆的位置关系,并说明理由。
,0)与以线段AB为直径的圆的位置关系,并说明理由。
科目:高中数学 来源: 题型:
【题目】(2015·新课标1卷)设函数f(x)=ex(2x-1)-ax+a,其中a<1,若存在唯一的整数x0 , 使得f(x0)<0,则a的取值范围是( )
A.[-![]() ,1)
,1)
B.[-![]() ,
,![]() )
)
C.[![]() ,
,![]() )
)
D.[![]() ,1)
,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)设fn(x)=x+x2+x...+xn-1, n![]() N, n≥2。
N, n≥2。
(1)fn'(2)
(2)证明:fn(x)在(0,![]() )内有且仅有一个零点(记为an), 且0<an-
)内有且仅有一个零点(记为an), 且0<an-![]() <
<![]() (
(![]() )n.
)n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)在一次马拉松比赛中,35名运动员的成绩(单位:分钟)如图I所示
若将运动员按成绩由好到差编为1~35号,再用系统抽样方法从中抽取7人,则其中成绩在区间[139,151]上的运动员人数为( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() ,m 是两条不同的直线,m 垂直于平面
,m 是两条不同的直线,m 垂直于平面![]() ,则“
,则“![]() ”是“
”是“![]() " 的 ( )
" 的 ( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·山东)设函数![]() =
=![]() . 已知曲线
. 已知曲线![]() = 在点
= 在点![]() 处的切线与直线
处的切线与直线![]() 平行.
平行.
(1)求![]() 的值;
的值;
(2)是否存在自然数![]() ,使得方程
,使得方程![]() =
=![]() 在
在![]() 内存在唯一的根?如果存在,求出k;如果不存在,请说明理由;
内存在唯一的根?如果存在,求出k;如果不存在,请说明理由;
(3)设函数![]() =
=![]()
![]() (
(![]() 表示,
表示,![]() 中的较小值),求
中的较小值),求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分15分)某工厂某种航空产品的年固定成本为![]() 万元,每生产
万元,每生产![]() 件,需另投入成本为
件,需另投入成本为![]() ,当年产量不足
,当年产量不足![]() 件时,
件时,![]() (万元).当年产量不小于
(万元).当年产量不小于![]() 件时,
件时,![]() (万元).每件商品售价为
(万元).每件商品售价为![]() 万元.通过市场分析,该厂生产的商品能全部售完.
万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (件)的函数解析式;
(件)的函数解析式;
(2)年产量为多少件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)设f(x)=lnx, 0<a<b,若p=f(![]() ),q=f(
),q=f(![]() ),r=
),r=![]() (f(a)+f(b)),则下列关系式中正确的是( )
(f(a)+f(b)),则下列关系式中正确的是( )
A.q=r<p
B.q=r>p
C.p=r<q
D.p=r>q
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com