
���� ��1����f��x��Ϊ���ֲ��溯����������ݶ�����֤�����Ƿ�������ɣ�
��2������f��x��Ϊ������R�ϵġ��ֲ��溯�����õ�f��-x��=-f��x���������������������ϵ������ʵ��m��ȡֵ��Χ��
��3������f��x��Ϊ������[-1��1]�ϵġ��ֲ��溯�����õ�f��-x��=-f��x���������������������ϵ������ʵ��a��ȡֵ��Χ��
��� �⣺��1����Ϊf��x��=x4+x3+x2+x-1��
����f��-x��=x4-x3+x2-x-1��
��f��-x��=-f��x����x4+x2-1=0��
��x2=t��[0��1]����t2+t-1=0����һ��$\frac{{\sqrt{5}-1}}{2}��[0��1]$��
������x��[-1��1]��ʹ��f��-x��=-f��x����
����f��x��Ϊ���ֲ��溯������
��2��������֪��g��-x��=-g��x����R���н⣬��4-x-2m•2-x+m2-3=-4x+2m•2x-m2+3��R���н⣬
����4x+4-x-2m��2x+2-x��+2��m2-3��=0��R���н⣬
��2x+2-x=u��[2��+�ޣ���
����u2-2mu+2m2-8=0��u��[2��+�ޣ����н⣬
��F��u��=u2-2mu+2m2-8��
�ٵ�F��2����0ʱ����2m2-4m-4��0�����$1-\sqrt{3}��m��1+\sqrt{3}$��
��ʱF��u����[2��+�ޣ��ϱ�����㣬����$1-\sqrt{3}��m��1+\sqrt{3}$��
�ڵ�F��2����0ʱ��F��u����[2��+�ޣ���������������
$\left\{{\begin{array}{l}{����0}\\{F��2����0}\\{�Գ���x=m��2}\end{array}}\right.⇒\left\{{\begin{array}{l}{4{m^2}-4��2{m^2}-8����0}\\{2{m^2}-4m-4��0}\\{m��2}\end{array}}\right.⇒1+\sqrt{3}��m��2\sqrt{2}$
���ϣ�$1-\sqrt{3}��m��2\sqrt{2}$��
��3��������֪��$?b��[1��\frac{3}{2}]$��-h��x��=h��-x����x��[-1��1]�϶��н⣬
��$?b��[1��\frac{3}{2}]$��ln��-x+1+a��+x2-x-b=-ln��x+1+a��-x2-x+b��x��[-1��1]�϶��н⣬
��$?b��[1��\frac{3}{2}]$��ln[��a+1��2-x2]+2x2=2b��x��[-1��1]�϶��н⣬
��x2=s��[0��1]����գ�s��=ln[��a+1��2-s]+2s��
������֪�գ�s����s��[0��1]�ϵ�ֵ�����[2��3]��
��Ϊ${��^'}��s��=\frac{-1}{{{{��a+1��}^2}-s}}+2$������Ϊs��[0��1]��a�ʣ�1��+�ޣ������ԣ�a+1��2-s��3��
���Ԧա䣨s����0�����Ԧգ�s����s��[0��1]�ϵ���������
����$\left\{{\begin{array}{l}{�գ�0����2}\\{�գ�1����3}\\{a��1}\end{array}}\right.⇒\left\{{\begin{array}{l}{a��e-1}\\{a��\sqrt{e+1}-1}\\{a��1}\end{array}}\right.⇒1��a��e-1$
���ϣ�1��a��e-1��
���� ������Ҫ�����뺯����ż���йص��¶��壬���������������̹�ϵ�ǽ������Ĺؼ�������ѧ���ļ�����������������


 ��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ�ļ������У��ı���ABCD�����Σ�ADNM�Ǿ��Σ�ƽ��ADNM��ƽ��ABCD����DAB=$\frac{��}{3}$��AD=4��AM=2��E��AB���е�
��ͼ��ʾ�ļ������У��ı���ABCD�����Σ�ADNM�Ǿ��Σ�ƽ��ADNM��ƽ��ABCD����DAB=$\frac{��}{3}$��AD=4��AM=2��E��AB���е��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a=-3��a=4 | B�� | -3��a��4 | C�� | a��4��a��-3 | D�� | a��R |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -7 | B�� | -6 | C�� | -3 | D�� | -1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
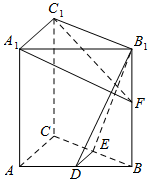 ��ͼ����ֱ������ABC-A1B1C1�У�D��E�ֱ�ΪAB��BC���е㣬��F�ڲ���B1B�ϣ���B1D��A1F��A1C1��A1B1����֤��
��ͼ����ֱ������ABC-A1B1C1�У�D��E�ֱ�ΪAB��BC���е㣬��F�ڲ���B1B�ϣ���B1D��A1F��A1C1��A1B1����֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ����ʱ�� �Ա� | ���� | ���� | �ϼ� |
| ��Ӥ | |||
| ŮӤ | |||
| �ϼ� |
| P��K2��k0�� | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 016 | B�� | 2 016 | C�� | -2 015 | D�� | 2 015 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com