
【题目】如图,在正方体![]() 中,点
中,点![]() 在线段
在线段![]() 上运动,则下列判断中不正确的是 ( )
上运动,则下列判断中不正确的是 ( )
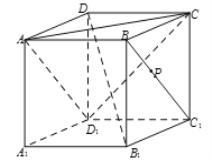
A. ![]() 与
与![]() 所成角的范围是
所成角的范围是![]()
B. ![]()
C. ![]()
D. 三棱锥![]() 的体积不变
的体积不变
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】已知 ![]() 是数列
是数列 ![]() 的前
的前 ![]() 项和,并且
项和,并且 ![]() ,对任意正整数
,对任意正整数 ![]() ,
, ![]() ,设
,设 ![]() (
( ![]() ).
).
(1)证明:数列 ![]() 是等比数列,并求
是等比数列,并求 ![]() 的通项公式;
的通项公式;
(2)设 ![]() ,求证:数列
,求证:数列 ![]() 不可能为等比数列.
不可能为等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均不相等的等差数列{an}的前n项和为Sn,S10=45,且a3,a5,a9恰为等比数列{bn}的前三项,记![]() .
.
(1)分别求数列{an}、{bn}的通项公式;
(2)若m=17,求cn取得最小值时n的值;
(3)当c1为数列{cn}的最小项时, ![]() 有相应的可取值,我们把所有am的和记为A1;…;当ci为数列
有相应的可取值,我们把所有am的和记为A1;…;当ci为数列![]() 的最小项时,
的最小项时,![]() 有相应的可取值,我们把所有am的和记为Ai;…,令Tn= A1+ A2+…+An,求Tn.
有相应的可取值,我们把所有am的和记为Ai;…,令Tn= A1+ A2+…+An,求Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且(c﹣2a) ![]() =c
=c ![]()
![]()
(1)求B的大小;
(2)已知f(x)=cosx(asinx﹣2cosx)+1,若对任意的x∈R,都有f(x)≤f(B),求函数f(x)的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+|x+5﹣a|
(1)若不等式f(x)﹣|x﹣a|≤2的解集为[﹣5,﹣1],求实数a的值;
(2)若x0∈R,使得f(x0)<4m+m2 , 求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com