
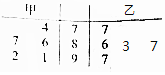
 某工厂组织工人技能培训,其中甲、乙两名技工在培训时进行的5次技能测试中的成绩如图茎叶图所示.
某工厂组织工人技能培训,其中甲、乙两名技工在培训时进行的5次技能测试中的成绩如图茎叶图所示.分析 (Ⅰ)由茎叶图分别求出甲、乙两人的平均数和方差,由此能求出结果.
(Ⅱ)甲高于85分的频率为$\frac{4}{5}$,每次成绩高于85分的概率$p=\frac{4}{5}$,由题意知ξ=0,1,2,3,由此能求出ξ的分布列及数学期望.
解答 解:(Ⅰ)$\overline{x_甲}=\frac{74+86+87+91+92}{5}=86,\overline{x_乙}=\frac{77+86+83+87+97}{5}=86$.
(2分)$s_甲^2=\frac{1}{5}[{(74-86)^2}+{(86-86)^2}+{(87-86)^2}+{(91-86)^2}+{(92-86)^2}]=41.2$,
$s_乙^2=\frac{1}{5}[{(77-86)^2}+{(86-86)^2}+{(83-86)^2}+{(87-86)^2}+{(97-86)^2}]=42.5$.(4分)
∵$\overline{{x_{甲}}}=\overline{x_乙},s_甲^2<s_乙^2$,∴派甲去更合适.(6分)
(Ⅱ)甲高于85分的频率为$\frac{4}{5}$,
∴每次成绩高于85分的概率$p=\frac{4}{5}$,
由题意知ξ=0,1,2,3,
$P(ξ=0)=C_3^0{(\frac{4}{5})^0}{(1-\frac{4}{5})^3}=\frac{1}{125}$,
P(ξ=1)=${C}_{3}^{1}(\frac{4}{5})(1-\frac{4}{5})^{2}$=$\frac{12}{125}$,
P(ξ=2)=${C}_{3}^{2}(\frac{4}{5})^{2}(1-\frac{4}{5})$=$\frac{48}{125}$,
$P(ξ=3)=C_3^3{(\frac{4}{5})^3}{(1-\frac{4}{5})^0}=\frac{64}{125}$(10分)
∴ξ分布列为
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{1}{125}$ | $\frac{12}{125}$ | $\frac{48}{125}$ | $\frac{64}{125}$ |
点评 本题考查茎叶图的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.


科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{1+\sqrt{3}}$ | B. | $\frac{{1+\sqrt{3}}}{2}$ | C. | $\frac{{2+\sqrt{3}}}{2}$ | D. | ±$\frac{{1+\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-1,\frac{1}{4})$ | B. | $({-∞,-1})∪(\frac{1}{4},+∞)$ | C. | $({-∞,-1}]∪[\frac{1}{4},+∞)$ | D. | $[-1,\frac{1}{4}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+2y-2=0 | B. | 2x-y+2=0 | C. | x-2y+2=0 | D. | 2x+y-2=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com