
 某市政府欲在如图所示的直角梯形ABCD的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),性状为直角梯形DEFG(线段ED和FG为两条底边),已知BC=2AB=2AD=4km,其中曲线AC是以A为顶点,AD为对称轴的抛物线的一部分.
某市政府欲在如图所示的直角梯形ABCD的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),性状为直角梯形DEFG(线段ED和FG为两条底边),已知BC=2AB=2AD=4km,其中曲线AC是以A为顶点,AD为对称轴的抛物线的一部分.分析 (1)建立坐标系,求出曲线AC的解析式,则所求面积等于梯形面积减去曲边三角形面积;
(2)设出F点横坐标a,将公园面积表示为a的函数,求出函数的最大值即可.
解答 解:(1)以AB为x轴,AD为y轴建立平面直角坐标系,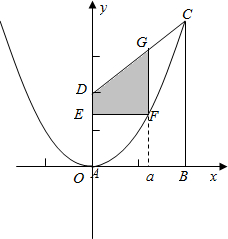
则A(0,0),B(2,0),C(2,4),D(0,2).
∴S梯形ABCD=$\frac{1}{2}$×(2+4)×2=6.
曲线AC的方程为y=x2,(0≤x≤2).
曲线AC与CD、AD所围成区域的面积为6-${∫}_{0}^{2}{x}^{2}dx$=6-$\frac{{x}^{3}}{3}$|$\underset{\stackrel{2}{\;}}{0}$=$\frac{10}{3}$.
(2)直线CD方程为$\frac{y-4}{2-4}=\frac{x-2}{0-2}$,即y=x+2,设点F横坐标为a,(0<a<$\sqrt{2}$).
则F(a,a2),G(a,a+2),E(0,a2).
∴DE=2-a2,EF=a,FG=a+2-a2,
则公园的面积为f(a)=$\frac{(2-{a}^{2}+a+2-{a}^{2})a}{2}$=-a3+$\frac{1}{2}$a2+2a.
∴f′(a)=-3a2+a+2.
令f′(a)=0得a1=-$\frac{2}{3}$(舍),a2=1.
当0<a<1时,f′(a)>0,当1≤a≤$\sqrt{2}$时,f′(a)<0,
∴f(a)在(0,1)上是增函数,在[1,$\sqrt{2}$)上是减函数.
∴fmax(a)=f(1)=$\frac{3}{2}$.
∴该公园的最大面积是$\frac{3}{2}$.
点评 本题考查了定积分的应和函数的最大值,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 若m⊥α,m⊥β,则α∥β | B. | 若α∩β=n,m∥n,则m∥α,m∥β | ||
| C. | 若m∥α,m⊥n,则n⊥α | D. | 若α⊥β,m⊥α,则m∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 46、45、56 | B. | 46、45、53 | C. | 47、45、56 | D. | 45、47、53 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com