
【题目】函数f(x)=ln(x2﹣x)的定义域为( )
A.(0,1)
B.[0,1]
C.(﹣∞,0)∪(1,+∞)
D.(﹣∞,0]∪[1,+∞)
科目:高中数学 来源: 题型:
【题目】命题p:x∈(﹣∞,0),2x>3x;命题q:x∈(0,+∞), ![]() >x3; 则下列命题中真命题是( )
>x3; 则下列命题中真命题是( )
A.p∧q
B.(¬p)∧q
C.(¬p)∨(¬q)
D.p∧(¬q)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=asinx﹣bcosx(a,b为常数,a≠0,x∈R)在x= ![]() 处取得最小值,则函数g(x)=f(
处取得最小值,则函数g(x)=f( ![]() ﹣x)是( )
﹣x)是( )
A.偶函数且它的图象关于点 (π,0)对称
B.奇函数且它的图象关于点 (π,0)对称
C.奇函数且它的图象关于点( ![]() . ,0)对称
. ,0)对称
D.偶函数且它的图象关于点( ![]() ,0)对称
,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min.在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运行的速度为130 m/min,山路AC长为1260 m,经测量,cos A=![]() ,cos C=
,cos C=![]()
(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若分别为P(1,0)、Q(2,0),R(4,0)、S(8,0)四个点各作一条直线,所得四条直线恰围成正方形,则该正方形的面积不可能为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数独游戏越来越受人们喜爱,今年某地区科技馆组织数独比赛,该区甲、乙、丙、丁四所学校的学生积极参赛,参赛学生的人数如表所示:
中学 | 甲 | 乙 | 丙 | 丁 |
人数 | 30 | 40 | 20 | 10 |
为了解参赛学生的数独水平,该科技馆采用分层抽样的方法从这四所中学的参赛学生中抽取30名参加问卷调查.
(Ⅰ)问甲、乙、丙、丁四所中学各抽取多少名学生?
(Ⅱ)从参加问卷调查的30名学生中随机抽取2名,求这2名学生来自同一所中学的概率;
(Ⅲ)在参加问卷调查的30名学生中,从来自甲、丙两所中学的学生中随机抽取2名,用X表示抽得甲中学的学生人数,求X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρsin(θ+ ![]() )=
)= ![]() .圆O的参数方程为
.圆O的参数方程为  (θ为参数,r>0).
(θ为参数,r>0).
(Ⅰ)求圆O的圆心的极坐标(ρ≥0,0≤θ<2π );
(Ⅱ)当r为何值时,圆O上的点到直线l的最大距离为2+ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,SB⊥底面ABC,且SB=AB=2,BC= ![]() ,D、E分别是SA、SC的中点.
,D、E分别是SA、SC的中点.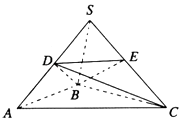
(I)求证:平面ACD⊥平面BCD;
(II)求二面角S﹣BD﹣E的平面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosx,sinx),
=(cosx,sinx), ![]() =(3,﹣
=(3,﹣ ![]() ),x∈[0,π].
),x∈[0,π].
(1)若 ![]() ∥
∥ ![]() ,求x的值;
,求x的值;
(2)记f(x)= ![]() ,求f(x)的最大值和最小值以及对应的x的值.
,求f(x)的最大值和最小值以及对应的x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com