
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 运用诱导公式化为cos100°=-cos80°,cos140°=-cos40°,再由80°=60°+20°,40°=60°-20°,运用两角和差的余弦公式,即可得到所求值.
解答 解:cos20°+cos60°+cos100°+cos140°
=cos20°+$\frac{1}{2}$-cos80°-cos40°
=cos20°+$\frac{1}{2}$-cos(60°+20°)-cos(60°-20°)
=cos20°+$\frac{1}{2}$-($\frac{1}{2}$cos20°-$\frac{\sqrt{3}}{2}$sin20°)-($\frac{1}{2}$cos20°+$\frac{\sqrt{3}}{2}$sin20°)
=cos20°+$\frac{1}{2}$-cos20°=$\frac{1}{2}$.
故选:B.
点评 本题考查诱导公式和两角和差的余弦公式,注意角的变换,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ③ | B. | ④ | C. | ①③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
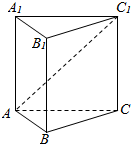 如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,直线AC1与平面BCC1B1所成角的余弦值等于( )
如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,直线AC1与平面BCC1B1所成角的余弦值等于( )| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\frac{\sqrt{5}}{4}$ | D. | $\frac{\sqrt{10}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com