
分析 由条件得到$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n+1}{n+2}$,利用累积法进行求解即可.
解答 解:∵(n+2)•an+1=(n+1)•an,
∴$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n+1}{n+2}$,
∴$\frac{{a}_{2}}{{a}_{1}}$=$\frac{2}{3}$,$\frac{{a}_{3}}{{a}_{2}}$=$\frac{3}{4}$,$\frac{{a}_{4}}{{a}_{3}}$=$\frac{4}{5}$,…$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n}{n+1}$,
等式两边同时相乘得$\frac{{a}_{2}}{{a}_{1}}$•$\frac{{a}_{3}}{{a}_{2}}$•$\frac{{a}_{4}}{{a}_{3}}$…•$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{2}{3}$•$\frac{3}{4}$•$\frac{4}{5}$…$\frac{n}{n+1}$,
即$\frac{{a}_{n}}{{a}_{1}}$=$\frac{2}{n+1}$,
即an=$\frac{2}{n+1}$•a1=$\frac{2}{n+1}$×1=$\frac{2}{n+1}$,
当n=1时,a1=1满足an=$\frac{2}{n+1}$,
故答案为:$\frac{2}{n+1}$.
点评 本题主要考查数列通项公式的求解,根据数列的递推关系利用累积法是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2015}{2016}$ | B. | $\frac{4028}{2015}$ | C. | $\frac{2015}{1008}$ | D. | $\frac{1007}{1008}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届广东华南师大附中高三综合测试一数学(文)试卷(解析版) 题型:解答题
设函数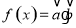 ,其中向量
,其中向量 .
.
(1)若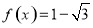 且
且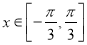 ,求
,求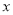 的值;
的值;
(2)若函数 的图象按向量
的图象按向量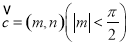 平移后得到函数
平移后得到函数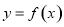 的图象,求实数
的图象,求实数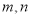 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com