
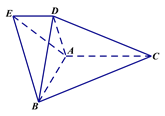
【题目】如图,在多面体![]() 中,平面
中,平面![]() ⊥平面
⊥平面![]() ,
,![]() ,
,![]() ,DE
,DE![]()
![]() AC,AD=BD=1.
AC,AD=BD=1.
(Ⅰ)求AB的长;
(Ⅱ)已知![]() ,求点E到平面BCD的距离的最大值.
,求点E到平面BCD的距离的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:(Ⅰ) 先由面面垂直的性质可得![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,可得
,可得![]() ,再证明
,再证明![]() 平面
平面![]() ,于是得
,于是得![]() ,由勾股定理可得结果;(Ⅱ)过
,由勾股定理可得结果;(Ⅱ)过![]() 作直线
作直线![]() ,以点
,以点![]() 为坐标原点,直线
为坐标原点,直线![]() 分别为
分别为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,如图所示. 记
,如图所示. 记![]() ,求出平面的一个法向量,利用点
,求出平面的一个法向量,利用点![]() 到平面
到平面![]() 的距离,结合
的距离,结合![]() ,可得点
,可得点![]() 到平面
到平面![]() 的距离的最大值.
的距离的最大值.
详解:(Ⅰ)∵平面ABD⊥平面ABC,且交线为AB,而AC⊥AB,∴AC⊥平面ABD.
又∵DE∥AC,∴DE⊥平面ABD,从而DE⊥BD.
注意到BD⊥AE,且DE∩AE=E,∴BD⊥平面ADE,于是,BD⊥AD.
而AD=BD=1,∴![]() .
.
(Ⅱ)∵AD=BD,取AB的中点为O,∴DO⊥AB.
又∵平面ABD⊥平面ABC,∴DO⊥平面ABC.
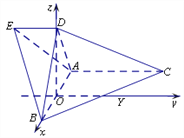
过O作直线OY∥AC,以点O为坐标原点,直线OB,OY,OD分别为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,如图所示.
,如图所示.
记![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
令平面BCD的一个法向量为![]() .
.
由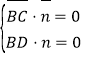 得
得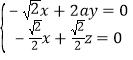 .令
.令![]() ,得
,得![]() .
.
又∵![]() ,∴点E到平面BCD的距离
,∴点E到平面BCD的距离 .
.
∵![]() ,∴当
,∴当![]() 时,
时,![]() 取得最大值,
取得最大值,![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】袋子![]() 和
和![]() 中均装有若干个大小相同的红球和白球,从
中均装有若干个大小相同的红球和白球,从![]() 中摸出一个红球的概率是
中摸出一个红球的概率是![]() ,从
,从![]() 中摸出一个红球的概率为
中摸出一个红球的概率为![]() .
.
(1)从![]() 中有放回地摸球,每次摸出1个,有3次摸到红球即停止,求恰好摸5次停止的概率.
中有放回地摸球,每次摸出1个,有3次摸到红球即停止,求恰好摸5次停止的概率.
(2)若![]() 、
、![]() 两个袋子中的球数之比为
两个袋子中的球数之比为![]() ,将
,将![]() 、
、![]() 中的球装在一起后,从中摸出一个红球的概率是
中的球装在一起后,从中摸出一个红球的概率是![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新个税法于2019年1月1日进行实施.为了调查国企员工对新个税法的满意程度,研究人员在![]() 地各个国企中随机抽取了1000名员工进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中
地各个国企中随机抽取了1000名员工进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中![]() .
.
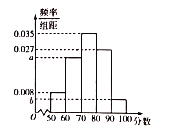
(1)求![]() 的值并估计被调查的员工的满意程度的中位数;(计算结果保留两位小数)
的值并估计被调查的员工的满意程度的中位数;(计算结果保留两位小数)
(2)若按照分层抽样从![]() ,
,![]() 中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在
中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(Ⅰ)若函数![]() 的图象在
的图象在![]() 处的切线为
处的切线为![]() ,当实数
,当实数![]() 变化时,求证:直线
变化时,求证:直线![]() 经过定点;
经过定点;
(Ⅱ)若函数![]() 有两个极值点,求实数
有两个极值点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
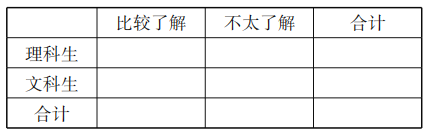
【题目】阿基米德是古希腊伟大的哲学家、数学家、物理学家,对几何学、力学等学科作出过卓越贡献.为调查中学生对这一伟大科学家的了解程度,某调查小组随机抽取了某市的100名高中生,请他们列举阿基米德的成就,把能列举阿基米德成就不少于3项的称为“比较了解”,少于三项的称为“不太了解”他们的调查结果如下:

(1)完成如下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为,了解阿基米德与选择文理科有关?
的把握认为,了解阿基米德与选择文理科有关?
(2)在抽取的100名高中生中,按照文理科采用分层抽样的方法抽取10人的样本.
(ⅰ)求抽取的文科生和理科生的人数;
(ⅱ)从10人的样本中随机抽取两人,求两人都是文科生的概率.
参考数据:

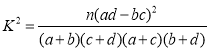 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com