
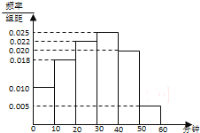
【题目】某电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了![]() 名观众进行调查,如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于
名观众进行调查,如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于![]() 分钟的观众称为体育迷.
分钟的观众称为体育迷.
(1)若日均收看该体育节目时间在![]() 内的观众中恰有两名女性,现日均收看时间在
内的观众中恰有两名女性,现日均收看时间在![]() 内的观众中抽取两名进行调查,求这两名观众恰好一男一女的概率;
内的观众中抽取两名进行调查,求这两名观众恰好一男一女的概率;
(2)若抽取![]() 人中有女性
人中有女性![]() 人,其中女体育迷有
人,其中女体育迷有![]() 人,完成答题卡中的列联表并判断能否在犯错误概率不超过
人,完成答题卡中的列联表并判断能否在犯错误概率不超过![]() 的前提下认为体育迷与性别有关系?
的前提下认为体育迷与性别有关系?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 |
|
| |
合计 |
附表及公式: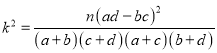 ,
,![]()
k0 | 2.706 | 3.841 | 6.635 |
【答案】(1) ![]() (2)列联表见解析,不能在犯错概率不超过
(2)列联表见解析,不能在犯错概率不超过![]() 的前提下认为体育迷与性别有关系.
的前提下认为体育迷与性别有关系.
【解析】
(1)先根据直方图求出日均收看时间在![]() 内的观众有5名,其中3男2女,再根据古典概型的概率公式可求得;
内的观众有5名,其中3男2女,再根据古典概型的概率公式可求得;
(2)求得观测值后,根据临界值表可得.
(1)由图可得,日均收看时间在![]() 内的观众有
内的观众有![]() 名,
名,
则其中有![]() 名男性,
名男性,![]() 名女性,
名女性,
记![]() 名男性为
名男性为![]() ,
,![]() ,
,![]() ,
,![]() 名女性为
名女性为![]() ,
,![]() .
.
从中抽取两名观众的情况有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共10种.
共10种.
其中恰好一男一女的情况有![]() 种,
种,
所以所求概率![]()
(2)由直方图可知,100名观众中体育迷观众有![]() 名,
名,
所以男体育迷有25-10=15,男非体育迷有45-15=30名.
所以![]() 列联表如下:
列联表如下:
非体育迷 | 体育迷 | 合计 | |
男 |
|
|
|
女 |
|
|
|
合计 |
|
|
|
![]()
故不能在犯错概率不超过![]() 的前提下认为体育迷与性别有关系.
的前提下认为体育迷与性别有关系.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,直线y=k(x+1)与C相切于点A,|AF|=2.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设直线l交C于M,N两点,T是MN的中点,若|MN|=8,求点T到y轴距离的最小值及此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某音乐院校举行“校园之星”评选活动,评委由本校全体学生组成,对![]() 两位选手,随机调查了20个学生的评分,得到下面的茎叶图:
两位选手,随机调查了20个学生的评分,得到下面的茎叶图:

所得分数 | 低于60分 | 60分到79分 | 不低于80分 |
分流方向 | 淘汰出局 | 复赛待选 | 直接晋级 |
(1)通过茎叶图比较![]() 两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
(2)举办方将会根据评分结果对选手进行三向分流,根据所得分数,估计![]() 两位选手中哪位选手直接晋级的概率更大,并说明理由.
两位选手中哪位选手直接晋级的概率更大,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为F,过点
的右焦点为F,过点![]() 的直线l与E交于A,B两点.当l过点F时,直线l的斜率为
的直线l与E交于A,B两点.当l过点F时,直线l的斜率为![]() ,当l的斜率不存在时,
,当l的斜率不存在时,![]() .
.
(1)求椭圆E的方程.
(2)以AB为直径的圆是否过定点?若过定点,求出定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A1,但不包括B1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在以直角坐标原点![]() 为极点,
为极点,![]() 的非负半轴为极轴的极坐标系下,曲线
的非负半轴为极轴的极坐标系下,曲线![]() 的方程是
的方程是![]() ,将
,将![]() 向上平移1个单位得到曲线
向上平移1个单位得到曲线![]() .
.
(Ⅰ)求曲线![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)若曲线![]() 的切线交曲线
的切线交曲线![]() 于不同两点
于不同两点![]() ,切点为
,切点为![]() .求
.求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 以
以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,设点
轴正半轴为极轴建立极坐标系,设点![]() 在曲线
在曲线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,且
上,且![]() 为正三角形.
为正三角形.
(1)求点![]() ,
,![]() 的极坐标;
的极坐标;
(2)若点![]() 为曲线
为曲线![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点,求
的中点,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com