
【题目】已知![]()
![]()
![]() ,若
,若![]() ,且
,且![]() 的图象相邻的对称轴间的距离不小于
的图象相邻的对称轴间的距离不小于![]() .
.
(1)求![]() 的取值范围.
的取值范围.
(2)若当![]() 取最大值时,
取最大值时, ![]() ,且在
,且在![]() 中,
中, ![]() 分别是角
分别是角![]() 的对边,其面积
的对边,其面积![]() ,求
,求![]() 周长的最小值.
周长的最小值.
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,其倾斜角为
,其倾斜角为![]() ,以原点
,以原点![]() 为极点,以
为极点,以![]() 轴为非负半轴为极轴,与坐标系
轴为非负半轴为极轴,与坐标系![]() 取相同的长度单位,建立极坐标系.设曲线
取相同的长度单位,建立极坐标系.设曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线![]() 与曲线
与曲线![]() 有公共点,求倾斜角
有公共点,求倾斜角![]() 的取值范围;
的取值范围;
(2)设![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
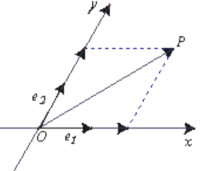
【题目】如图,设![]() 是平面内相交成
是平面内相交成![]() 角的两条数轴 ,
角的两条数轴 ,![]() 分别是
分别是![]() 轴,
轴,![]() 轴正方向同向的单位向量,若向量
轴正方向同向的单位向量,若向量![]() ,则把有序数对
,则把有序数对![]() 叫做向量
叫做向量![]() 在坐标系
在坐标系![]() 中的坐标,假设
中的坐标,假设![]() .
.
(1)计算![]() 的大小;
的大小;
(2)设向量![]() ,若
,若![]() 与
与![]() 共线,求实数
共线,求实数![]() 的值;
的值;
(3)是否存在实数![]() ,使得
,使得![]() 与向量
与向量![]() 垂直,若存在求出
垂直,若存在求出![]() 的值,若不存在请说明理由.
的值,若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)已知函数f(x)=ex, g(x)=lnx.
(1)设f(x)在x1处的切线为l1, g(x)在x2处的切线为l2,若l1//l2,求x1+g(x2)的值;
(2)若方程af 2(x)-f(x)-x=0有两个实根,求实数a的取值范围;
(3)设h(x)=f(x)(g(x)-b),若h(x)在[ln2,ln3]内单调递减,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过
,过![]() 且垂直于
且垂直于![]() 轴的焦点弦的弦长为
轴的焦点弦的弦长为![]() ,过
,过![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() ,
,![]() 互相垂直,直线
互相垂直,直线![]() 过
过![]() 且与椭圆
且与椭圆![]() 交于点
交于点![]() ,
,![]() 两点,直线
两点,直线![]() 过
过![]() 且与椭圆
且与椭圆![]() 交于
交于![]() ,
,![]() 两点.求
两点.求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过
,过![]() 且垂直于
且垂直于![]() 轴的焦点弦的弦长为
轴的焦点弦的弦长为![]() ,过
,过![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() ,
,![]() 互相垂直,直线
互相垂直,直线![]() 过
过![]() 且与椭圆
且与椭圆![]() 交于点
交于点![]() ,
,![]() 两点,直线
两点,直线![]() 过
过![]() 且与椭圆
且与椭圆![]() 交于
交于![]() ,
,![]() 两点.求
两点.求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 中,底面
中,底面![]() 是菱形,侧面
是菱形,侧面![]() 平面
平面![]() ,且
,且![]() ,
,![]() ,
,![]() .
.

(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)若点![]() 在线段
在线段![]() 上,且
上,且![]() ,试问:在
,试问:在![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 面
面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.

(Ⅰ)求证:AA1⊥平面ABC;
(Ⅱ)求二面角A1-BC1-B1的余弦值;
(Ⅲ)证明:在线段BC1存在点D,使得AD⊥A1B,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 某创业投资公司拟投资开发某种新能源产品,估计能获得25万元~ 1600万元的投资收益,现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,奖金不超过75万元,同时奖金不超过投资收益的20%.(即:设奖励方案函数模型为y=f (x)时,则公司对函数模型的基本要求是:当x∈[25,1600]时,①f(x)是增函数;②f (x) ![]() 75恒成立;
75恒成立; ![]()
![]() 恒成立.
恒成立.
(1)判断函数![]() 是否符合公司奖励方案函数模型的要求,并说明理由;
是否符合公司奖励方案函数模型的要求,并说明理由;
(2)已知函数![]() 符合公司奖励方案函数模型要求,求实数a的取值范围.
符合公司奖励方案函数模型要求,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com