练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图所示，梯形是平面图形的直观图.其中.

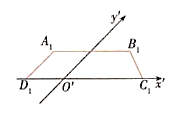
    （1）如何利用斜二测画法的规则画出原四边形？

    （2）在问题（1）中，如何求出水平放置的平面图形与直观图的面积？

    【答案】（1）见解析 ；（2）水平放置的平面图形的面积是5，直观图的面积是，详见解析.

    【解析】

    （1）利用斜二测画法的规则进行还原，与轴平行的线段，平行关系和长度关系不变，与轴平行的线段，平行关系不变，长度关系要变为2倍；

    （2）根据梯形的面积公式进行求解.

    （1）如图，建立平面直角坐标系，在轴上截取.

    在过点的轴的平行线上截取.在过点的轴的平行线上截取.连接，即得到了原图形.

    （2）由作法可知，原四边形是直角梯形，上，下底边长度分别为，直角腰的长度，所以面积为.

    易得直观图中梯形的高为，因此其面积为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，直三棱柱ABC-A1B1C1中，D,E分别是AB，BB1的中点.

    （Ⅰ）证明： BC1//平面A1CD;

    （Ⅱ）设AA1= AC=CB=2，AB=2，求三棱锥C一A1DE的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在抗击新型冠状病毒肺炎期间，为响应政府号召，郴州市某单位组织了志愿者30人，其中男志愿者18人，用分层抽样的方法从该单位志愿者中抽取5人去参加某社区的防疫帮扶活动．

    （1）求从该单位男、女志愿者中各抽取的人数；

    （2）从抽取的5名志愿者中任选2名谈此活动的感受，求选出的2名志愿者中恰有1名男志愿者的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知袋子中放有大小和形状相同的小球若干，其中标号为0的小球1个，标号为1的小球1个，标号为2的小球个.若从袋子中随机抽取1个小球，取到标号为2的小球的概率是.

    （1）求的值；

    （2）从袋子中不放回地随机抽取2个小球，记第一次取出的小球标号为，第二次取出的小球标号为.

    ①记“”为事件，求事件的概率；

    ②在区间内任取2个实数，，求事件“恒成立”的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数f（x）=﹣x﹣cos2x+m（sinx﹣cosx）在（﹣∞，+∞）上单调递减，则m的取值范围是____________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将函数y=2cos（2x+）的图象向左平移个单位长度，得到函数y=f（x）的图象．

    （1）求f（x）的单调递增区间；

    （2）求f（x）在[0，]上的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某地一天从时的温度变化曲线近似满足函数.

    （1）求该地区这一段时间内温度的最大温差.

    （2）若有一种细菌在到之间可以生存，则在这段时间内，该细菌最多能存活多长时间？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知.

    （1）求的解析式；

    （2）求时，的值域：

    （3）设，若对任意的，总有恒成立，求实数a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】通过市场调查，得到某种产品的资金投入（单位：万元）与获得的利润（单位：千元）的数据，如表所示

    资金投入

    2

    3

    4

    5

    利润

    2

    3

    5

    6

    （1）根据上表提供的数据，用最小二乘法求线性回归直线方程；

    （2）该产品的资金投入每增加万元，获得利润预计可增加多少千元？若投入资金万元，则获得利润的估计值为多少千元？

    参考公式：

    查看答案和解析>>

    同步练习册答案