
(本题满分14分)
制订投资计划时,不仅要考虑可能要获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目,根据预测,甲、乙项目可能的最大盈利分别为100%和50%,可能的最大亏损率分别为30%和10%,投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元,问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
投资人用4万元投资甲项目,6万元投资乙项目,才能确保亏损不超过1.8万元的前提下,使可能的盈利最大.
解析试题分析:解:设投资人分别用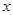 万元,
万元, 万元投资
万元投资
甲、乙两个项目,由题意知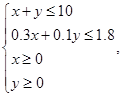
目标函数 ,上述不等式组表示的平面区域如图所示,阴影部分(含边界)即可行域.
,上述不等式组表示的平面区域如图所示,阴影部分(含边界)即可行域.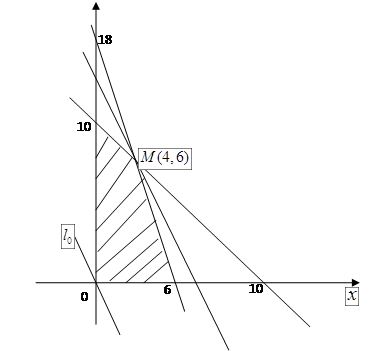
作直线 ,并作出平行于直线
,并作出平行于直线 的一组直线
的一组直线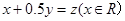 与可行域相交,其中有一条直线经过可行域上的
与可行域相交,其中有一条直线经过可行域上的 点,且与直线
点,且与直线 的距离最大,这里
的距离最大,这里 点是直线
点是直线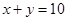 和
和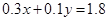 的交点.
的交点.
解方程组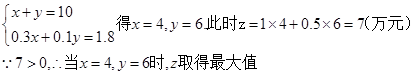
答:投资人用4万元投资甲项目,6万元投资乙项目,才能确保亏损不超过1.8万元的前提下,使可能的盈利最大.
考点:线性规划的实际运用
点评:解决该试题的关键是能根据已知的实际变量,找到不等式组,结合不等式组表示的区域,和目标函数平移法得到结论,属于基础题。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
在中,记(角的单位是弧度制),的面积为S,且
.
(1)求的取值范围;
(2)就(1)中的取值范围,求函数的最大值、最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
在中,记(角的单位是弧度制),的面积为S,且
.
(1)求的取值范围;
(2)就(1)中的取值范围,求函数的最大值、最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com