
【题目】在平面直角坐标系![]() 中,设
中,设![]() 为边长为1的正方形内部及其边界的点构成的集合.从
为边长为1的正方形内部及其边界的点构成的集合.从![]() 中的任意点P作x轴、y轴的垂线,垂足分别为
中的任意点P作x轴、y轴的垂线,垂足分别为![]() ,
,![]() .所有点
.所有点![]() 构成的集合为M,M中所有点的横坐标的最大值与最小值之差记为
构成的集合为M,M中所有点的横坐标的最大值与最小值之差记为![]() ;所有点
;所有点![]() 构成的集合为N,N中所有点的纵坐标的最大值与最小值之差记为
构成的集合为N,N中所有点的纵坐标的最大值与最小值之差记为![]() .给出以下命题:
.给出以下命题:
①![]() 的最大值为
的最大值为![]() :②
:②![]() 的取值范围是
的取值范围是![]() ;③
;③![]() 恒等于0.
恒等于0.
其中所有正确结论的序号是()
A.①②B.②③C.①③D.①②③
科目:高中数学 来源: 题型:
【题目】在如图的程序框图中,若输入![]() ,
,![]() ,则输出的
,则输出的![]() 值是( )
值是( )
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/3/21/1907086498037760/1907898837975040/STEM/25d20caaa911497ea3baaf4f7dee45a3.png]
A. 3 B. 7 C. 11 D. 33
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着国内电商的不断发展,快递业也进入了高速发展时期,按照国务院的发展战略布局,以及国家邮政管理总局对快递业的宏观调控,SF快递收取快递费的标准是:重量不超过1kg的包裹收费10元;重量超过1kg的包裹,在收费10元的基础上,每超过1kg(不足1kg,按1kg计算)需再收5元.某县SF分代办点将最近承揽的100件包裹的重量统计如下:
重量(单位:kg) | (0,1] | (1,2] | (2,3] | (3,4] | (4,5] |
件数 | 43 | 30 | 15 | 8 | 4 |
对近60天,每天揽件数量统计如下表:
件数范围 | 0~100 | 101~200 | 201~300 | 301~400 | 401~500 |
件数 | 50 | 150 | 250 | 350 | 450 |
天数 | 6 | 6 | 30 | 1 | 6 |
以上数据已做近似处理,将频率视为概率.
(1)计算该代办未来5天内不少于2天揽件数在101~300之间的概率;
(2)①估计该代办点对每件包裹收取的快递费的平均值;
②根据以往的经验,该代办点将快递费的三分之一作为前台工作人员的工资和公司利润,其余的用作其他费用.目前该代办点前台有工作人员3人,每人每天揽件不超过150件,日工资110元.代办点正在考虑是否将前台工作人员裁减1人,试计算裁员前后代办点每日利润的数学期望,若你是决策者,是否裁减工作人员1人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市采购了一批袋装的进口牛肉干进行销售,共1000袋,每袋成本为30元,销售价格为50元,经过科学测定,每袋牛肉干变质的概率为![]() ,且各袋牛肉干是否变质相互独立.依据消费者权益保护法的规定:超市出售变质食品的,消费者可以要求超市退一赔三.为了保护消费者权益,针对购买到变质牛肉干的消费者,超市除退货外,并对每袋牛肉干以销售价格的三倍现金赔付,且把变质牛肉干做废物处理,不再进行销售.
,且各袋牛肉干是否变质相互独立.依据消费者权益保护法的规定:超市出售变质食品的,消费者可以要求超市退一赔三.为了保护消费者权益,针对购买到变质牛肉干的消费者,超市除退货外,并对每袋牛肉干以销售价格的三倍现金赔付,且把变质牛肉干做废物处理,不再进行销售.
(1)若销售完这批牛肉干后得到的利润为X,且![]() ,求p的取值范围;
,求p的取值范围;
(2)已知![]() ,若超市聘请兼职员工来检查这批牛肉干是否变质,超市需要支付兼职员工工资5000元,这样检查到的变质牛肉干直接当废物处理,就不会流入到消费者手中.请以超市获取的利润为决策依据,判断超市是否需要聘请兼职员工来检验这批牛肉干是否变质?
,若超市聘请兼职员工来检查这批牛肉干是否变质,超市需要支付兼职员工工资5000元,这样检查到的变质牛肉干直接当废物处理,就不会流入到消费者手中.请以超市获取的利润为决策依据,判断超市是否需要聘请兼职员工来检验这批牛肉干是否变质?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程是
的参数方程是 (
(![]() 为参数).
为参数).
(Ⅰ)将曲线![]() ,
,![]() 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)求曲线![]() 上的点到曲线
上的点到曲线![]() 的距离的最大值和最小值.
的距离的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.
①当x=10时,顾客一次购买草莓和西瓜各1盒,需要支付__________元;
②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() .
.
(1)若直线![]() 经过抛物线
经过抛物线![]() 的焦点,求抛物线
的焦点,求抛物线![]() 的准线方程;
的准线方程;
(2)若斜率为-1的直线经过抛物线![]() 的焦点
的焦点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() ,
,![]() 两点,当
两点,当![]() 时,求抛物线
时,求抛物线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某沿海地区计划铺设一条电缆联通A,B两地,A地位于东西方向的直线MN上的陆地处,B地位于海上一个灯塔处,在A地用测角器测得![]() ,在A地正西方向4km的点C处,用测角器测得
,在A地正西方向4km的点C处,用测角器测得![]() .拟定铺设方案如下:在岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设.预算地下、水下的电缆铺设费用分别为2万元/km和4万元/km,设
.拟定铺设方案如下:在岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设.预算地下、水下的电缆铺设费用分别为2万元/km和4万元/km,设![]() ,
,![]() ,铺设电缆的总费用为
,铺设电缆的总费用为![]() 万元.
万元.
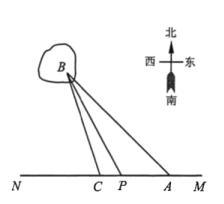
(1)求函数![]() 的解析式;
的解析式;
(2)试问点P选在何处时,铺设的总费用最少,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com