
【题目】已知函数f(x)= ![]() 的定义域为A.
的定义域为A.
(1)求A;
(2)已知k>0,集合B={x| ![]() },且A∩B≠,求实数k的取值范围.
},且A∩B≠,求实数k的取值范围.
【答案】
(1)解:由题意,得 ![]() ,解得﹣3<x<0,或2<x<3,
,解得﹣3<x<0,或2<x<3,
∴函数的定义域为A={x|﹣3<x<0或2<x<3}.
(2)解:∵x2﹣2x+1﹣k2≥0,
∴当k>0时,x≤1﹣k,或x≥1+k
又x>1,∴x≥1+k,
∴B={x|x≥1+k},
又∵A∩B≠,
∴ ![]() ,∴0<k<2,
,∴0<k<2,
∴实数k的取值范围为0<k<2.
【解析】(1)由题意,得 ![]() ,解得即可,(2)求出集合B,再根据A∩B≠,即可求出a的范围.
,解得即可,(2)求出集合B,再根据A∩B≠,即可求出a的范围.
【考点精析】通过灵活运用集合的交集运算和函数的定义域及其求法,掌握交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立;求函数的定义域时,一般遵循以下原则:①
B,反之也成立;求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零即可以解答此题.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零即可以解答此题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】某特色餐馆开通了美团外卖服务,在一周内的某特色菜外卖份数![]() (份)与收入
(份)与收入![]() (元)之间有如下的对应数据:
(元)之间有如下的对应数据:
外卖份数 | 2 | 4 | 5 | 6 | 8 |
收入 | 30 | 40 | 60 | 50 | 70 |
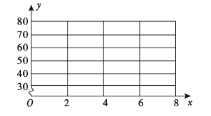
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计外卖份数为12份时,收入为多少元.
注:①参考公式:线性回归方程系数公式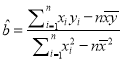 ,
, ![]() ;
;
②参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 直线l经过F2且交椭圆C于A,B两点(如图),△ABF1的周长为4
=1(a>b>0)的左、右焦点分别为F1 , F2 , 直线l经过F2且交椭圆C于A,B两点(如图),△ABF1的周长为4 ![]() ,原点O到直线l的最大距离为1.
,原点O到直线l的最大距离为1. 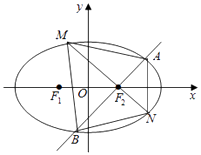
(1)求椭圆C的标准方程;
(2)过F2作弦AB的垂线交椭圆C于M,N两点,求四边形AMBN面积最小时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 满足:(1)截
满足:(1)截![]() 轴所得弦长为2;(2)被
轴所得弦长为2;(2)被![]() 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为![]() .在满足条件(1)、(2)的所有圆中,圆心到直线
.在满足条件(1)、(2)的所有圆中,圆心到直线![]() 的距离最小的圆的方程为__________.
的距离最小的圆的方程为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图四边形ABCD为梯形,AD∥BC,∠ABC=90°,AD=2,AB=4,BC=5,图中阴影部分(梯形剪去一个扇形)绕AB旋转一周形成一个旋转体.
(1)求该旋转体的表面积;
(2)求该旋转体的体积. 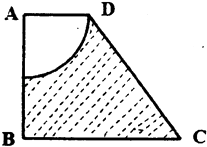
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点. 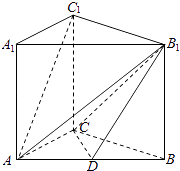
(1)求证:AC1∥平面CDB1
(2)求证:AC⊥BC1
(3)求直线AB1与平面BB1C1C所成的角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
| 上一个年度未发生有责任道路交通事故 | 下浮10% |
| 上两个年度未发生有责任道路交通事故 | 下浮20% |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
|
|
数量 | 10 | 5 | 5 | 20 | 15 | 5 |
以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
![]() 求一辆普通6座以下私家车(车险已满三年)在下一年续保时保费高于基本保费的频率;
求一辆普通6座以下私家车(车险已满三年)在下一年续保时保费高于基本保费的频率;
![]() 某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元.且各种投保类型车的频率与上述机构调查的频率一致,完成下列问题:
某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元.且各种投保类型车的频率与上述机构调查的频率一致,完成下列问题:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选两辆车,求这两辆车恰好有一辆为事故车的概率;
②若该销售商一次购进120辆(车龄已满三年)该品牌二手车,求一辆车盈利的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若a,b是函数f(x)=x2﹣px+q(p>0,q>0)的两个不同的零点,且a,b,﹣2这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p+q的值等于 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com