【答案】
分析:(1)由f(x)≤0的解集有且只有一个元素可知△=a
2-4a=0,从而可求得a值,又定义域内存在0<x
1<x
2,使得不等式f(x
1)>f(x
2)成立,对a进行检验取舍,可确定a值,利用S
n与a
n的关系即可求得a
n.
(2)由(1)求得b
n,根据其结构特征利用错位相减法即可求得T
n;
(3)先求出C
n,判断n≥3时数列的单调性,根据变号数的定义可得n≥3时的变号数,根据c
1=-3,c
2=5,c
3=-3,可得此处变号数,从而可求得数列{c
n}的变号数.
解答:解:(1)∵f(x)≤0的解集有且只有一个元素,
∴△=a
2-4a=0⇒a=0或a=4,
当a=0时,函数f(x)=x
2在(0,+∞)上递增,
故不存在0<x
1<x
2,使得不等式f(x
1)>f(x
2)成立,
当a=4时,函数f(x)=x
2-4x+4在(0,2)上递减,
故存在0<x
1<x
2,使得不等式f(x
1)>f(x
2)成立.
综上,得a=4,f(x)=x
2-4x+4,
∴
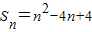
,
∴

;
(2)∵
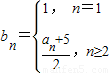
=
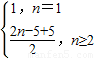
,
∴b
n=n,
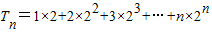
,①

,②
①-②得,-T
n=2+2
2+…+2
n-n•2
n+1=
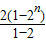
-n•2
n+1,
∴

;
(3)由题设

∵n≥3时,

,
∴n≥3时,数列{c
n}递增,
∵

,由
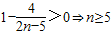
,
可知a
4•a
5<0,即n≥3时,有且只有1个变号数;
又∵c
1=-3,c
2=5,c
3=-3,
即c
1•c
2<0,c
2•c
3<0,
∴此处变号数有2个.
综上得 数列{c
n}共有3个变号数,即变号数为3;
点评:本题考查数列与函数的综合,考查学生综合运用所学知识分析问题解决问题的能力,考查学生解决新问题的能力,综合性强,难度大,对能力要求高.

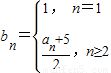 ,Tn=
,Tn=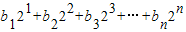 ,求Tn;
,求Tn;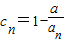 (n为正整数),求数列{cn}的变号数.
(n为正整数),求数列{cn}的变号数.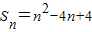 ,
, ;
;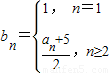 =
=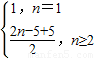 ,
,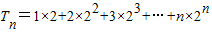 ,①
,① ,②
,②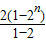 -n•2n+1,
-n•2n+1, ;
;
 ,
, ,由
,由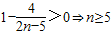 ,
,

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案