
 如图所示,在正方体ABCD-A1B1C1D1中,E在A1D1上,且$\overrightarrow{{A}_{1}E}=2\overrightarrow{E{D}_{1}}$,F在对角线A1C上,且$\overrightarrow{{A}_{1}F}=\frac{2}{3}\overrightarrow{FC}$.求证:E,F,B三点共线.
如图所示,在正方体ABCD-A1B1C1D1中,E在A1D1上,且$\overrightarrow{{A}_{1}E}=2\overrightarrow{E{D}_{1}}$,F在对角线A1C上,且$\overrightarrow{{A}_{1}F}=\frac{2}{3}\overrightarrow{FC}$.求证:E,F,B三点共线. 分析 根据题意,建立空间直角坐标系O-xyz,写出点的坐标,求出向量$\overrightarrow{BF}$、$\overrightarrow{BE}$与$\overrightarrow{FE}$,利用向量共线证明E,F,B三点共线.
解答 解:根据题意,建立空间直角坐标系O-xyz,如图所示: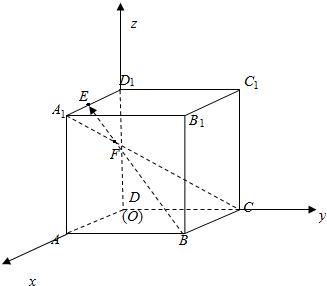
则D(0,0,0),B(1,1,0),A1(1,0,1),C(0,1,0),D1(0,0,1);
∵E在A1D1上,且$\overrightarrow{{A}_{1}E}=2\overrightarrow{E{D}_{1}}$,
∴E($\frac{1}{3}$,0,1);
且F在对角线A1C上,且$\overrightarrow{{A}_{1}F}=\frac{2}{3}\overrightarrow{FC}$,
∴$\overrightarrow{OF}$-$\overrightarrow{{OA}_{1}}$=$\frac{2}{3}$($\overrightarrow{OC}$-$\overrightarrow{OF}$),
∴$\overrightarrow{OF}$=$\frac{3}{5}$$\overrightarrow{{OA}_{1}}$+$\frac{2}{5}$$\overrightarrow{OC}$=($\frac{3}{5}$,0,$\frac{3}{5}$)+(0,$\frac{2}{5}$,0),
即F($\frac{3}{5}$,$\frac{2}{5}$,$\frac{3}{5}$);
∴$\overrightarrow{BF}$=(-$\frac{2}{5}$,-$\frac{3}{5}$,$\frac{3}{5}$),
$\overrightarrow{BE}$=(-$\frac{2}{3}$,-1,1),
$\overrightarrow{FE}$=(-$\frac{4}{15}$,-$\frac{2}{5}$,$\frac{2}{5}$),
∴$\overrightarrow{BE}$=$\overrightarrow{BF}$+$\overrightarrow{FE}$,
∴E,F,B三点共线.
点评 本题考查了空间向量的应用问题,也考查了三点共线的证明问题,考查了空间想象能力与逻辑思维能力,是综合性题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | [15,+∞) | B. | (-∞,19] | C. | (15,19) | D. | [15,19] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在△OAB中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,点M是AB的靠近B的一个三等分点,点N是OA的靠近A的一个四等分点,若OM与BN相交于点P,求$\overrightarrow{OP}$.
如图所示,在△OAB中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,点M是AB的靠近B的一个三等分点,点N是OA的靠近A的一个四等分点,若OM与BN相交于点P,求$\overrightarrow{OP}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{2}{e}$] | B. | (-∞,$\frac{2}{e}$) | C. | (-∞,0] | D. | (-∞,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com