
【题目】在直角坐标系xOy中,圆C的参数方程 ![]() 为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.
为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求圆C的极坐标方程;
(2)直线l的极坐标方程是 ![]() ,射线
,射线 ![]() 与圆C的交点为O,P,与直线l的交点为Q,求|OP||OQ|的范围.
与圆C的交点为O,P,与直线l的交点为Q,求|OP||OQ|的范围.
【答案】
(1)解:∵圆C的参数方程 ![]() 为参数),
为参数),
∴消去参数φ,得圆C的普通方程是(x﹣1)2+y2=1,
又x=ρcosθ,y=ρsinθ,
∴圆C的极坐标方程是ρ=2cosθ.
(2)解:设P(ρ1,θ1),则有ρ1=2cosθ1,Q(ρ2,θ1),
则有 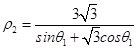 ,
,
∴  ,
,
∵tanθ1>0,∴0<|OP||OQ|<6.
故|OP||OQ|的范围是(0,6).
【解析】(1)圆C的参数方程消去参数φ,能求出圆C的普通方程,再由x=ρcosθ,y=ρsinθ,能求出圆C的极坐标方程.(2)设P(ρ1,θ1),则有ρ1=cosθ1,Q(ρ2,θ1),则 ![]() ,|OP||OQ|=ρ1ρ2,结合tanθ1>0,能求出|OP||OQ|的范围.
,|OP||OQ|=ρ1ρ2,结合tanθ1>0,能求出|OP||OQ|的范围.


科目:高中数学 来源: 题型:
【题目】已知一个几何体的三视图如图所示.

(1)求此几何体的表面积;
(2)如果点![]() 在正视图中所示位置:
在正视图中所示位置:![]() 为所在线段中点,
为所在线段中点,![]() 为顶点,求在几何体表面上,从
为顶点,求在几何体表面上,从![]() 点到
点到![]() 点的最短路径的长.
点的最短路径的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin( ![]() +x)(cosx﹣2sinx)+sin2x的图象向左平移
+x)(cosx﹣2sinx)+sin2x的图象向左平移 ![]() 个单位长度后得到函数g(x),则g(x)具有性质( )
个单位长度后得到函数g(x),则g(x)具有性质( )
A.在(0, ![]() )上单调递增,为奇函数
)上单调递增,为奇函数
B.周期为π,图象关于( ![]() )对称
)对称
C.最大值为 ![]() ,图象关于直线x=
,图象关于直线x= ![]() 对称
对称
D.在(﹣ ![]() )上单调递增,为偶函数
)上单调递增,为偶函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为  (t为参数),在以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ=2
(t为参数),在以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ=2 ![]() cos(
cos( ![]() +θ).
+θ).
(I)求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)设直线l与曲线C相交于M,N两点,求|MN|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,已知向量 ![]() 与
与 ![]() 平行.
平行.
(1)求 ![]() 的值;
的值;
(2)若bcosC+ccosB=1,△ABC周长为5,求b的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县一中计划把一块边长为20米的等边三角形ABC的边角地辟为植物新品种实验基地,图中DE需把基地分成面积相等的两部分,D在AB上,E在AC上. 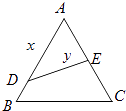
(1)设AD=x(x≥10),ED=y,试用x表示y的函数关系式;
(2)如果DE是灌溉输水管道的位置,为了节约,则希望它最短,DE的位置应该在哪里?如果DE是参观线路,则希望它最长,DE的位置又应该在哪里?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,O为总信号源点,A,B,C是三个居民区,已知A,B都在O的正东方向上,OA=10km,OB=20km,C在O的北偏西45°方向上,CO=5 ![]() km.
km. 
(1)求居民区A与C的距离;
(2)现要经过点O铺设一条总光缆直线EF(E在直线OA的上方),并从A,B,C分别铺设三条最短分光缆连接到总光缆EF.假设铺设每条分光缆的费用与其长度的平方成正比,比例系数为m(m为常数).设∠AOE=θ(0≤θ<π),铺设三条分光缆的总费用为w(元). ①求w关于θ的函数表达式;
②求w的最小值及此时tanθ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙、丙、丁四位同学中选拔一位成绩较稳定的优秀选手,参加山东省职业院校技能大赛,在同样条件下经过多轮测试,成绩分析如表所示,根据表中数据判断,最佳人选为( ) 成绩分析表
甲 | 乙 | 丙 | 丁 | |
平均成绩 | 96 | 96 | 85 | 85 |
标准差s | 4 | 2 | 4 | 2 |
A.甲
B.乙
C.丙
D.丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com