
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示,下列说法正确的是( )
)的部分图象如图所示,下列说法正确的是( ) 
A.函数f(x)的图象关于直线x=﹣ ![]() 对称
对称
B.函数f(x)的图象关于点(﹣ ![]() ,0)对称
,0)对称
C.若方程f(x)=m在[﹣ ![]() ,0]上有两个不相等的实数根,则实数m∈(﹣2,﹣
,0]上有两个不相等的实数根,则实数m∈(﹣2,﹣ ![]() ]
]
D.将函数f(x)的图象向左平移 ![]() 个单位可得到一个偶函数
个单位可得到一个偶函数
【答案】C
【解析】解:根据函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象,可得A=2,
)的部分图象,可得A=2, ![]() =
= ![]() ﹣
﹣ ![]() ,∴ω=2. 再根据五点法作图,可得2
,∴ω=2. 再根据五点法作图,可得2 ![]() +φ=π,∴φ=
+φ=π,∴φ= ![]() ,f(x)=2sin(2x+
,f(x)=2sin(2x+ ![]() ).
).
当x=﹣ ![]() 时,f(x)=0,不是最值,故函数f(x)的图象不关于直线x=﹣
时,f(x)=0,不是最值,故函数f(x)的图象不关于直线x=﹣ ![]() 对称,故排除A;
对称,故排除A;
当x=﹣ ![]() 时,f(x)=﹣2,是最值,故函数f(x)的图象关于直线x=﹣
时,f(x)=﹣2,是最值,故函数f(x)的图象关于直线x=﹣ ![]() 对称,故排除B;
对称,故排除B;
在[﹣ ![]() ,0]上,2x+
,0]上,2x+ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],方程f(x)=m在[﹣
],方程f(x)=m在[﹣ ![]() ,0]上有两个不相等的实数根,则实数m∈(﹣2,﹣
,0]上有两个不相等的实数根,则实数m∈(﹣2,﹣ ![]() ],故C正确;
],故C正确;
将函数f(x)的图象向左平移 ![]() 个单位,可得y=2sin(2x+
个单位,可得y=2sin(2x+ ![]() +
+ ![]() )=﹣sin2x 的图象,故所得函数为奇函数,故排除D,
)=﹣sin2x 的图象,故所得函数为奇函数,故排除D,
故选:C.
由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得f(x)的解析式;再利用正弦函数的定义域和值域,正弦函数的图象和性质,判断各个选项是否正确,从而得出结论.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】我市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
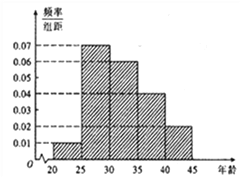
(1)分别求第3,4,5组的频率.
(2)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加广场宣传活动,应从第3,4,5组各抽取多少名志愿者?
(3)在(2)的条件下,我市决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于![]() 个黑球和
个黑球和![]() 个白球的任意排列(从左到右排成一行),则一定( )
个白球的任意排列(从左到右排成一行),则一定( )
A. 存在一个白球,它右侧的白球和黑球一样多
B. 存在一个黑球,它右侧的白球和黑球一样多
C. 存在一个白球,它右侧的白球比黑球少一个
D. 存在一个黑球,它右侧的白球比黑球少一个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点列An(xn , 0),n∈N* , 其中x1=0,x2=1.A3是线段A1A2的中点,A4是线段A2A3的中点,…,An+2是线段AnAn+1的中点,…设an=xn+1﹣xn . (Ⅰ)写出xn与xn﹣1、xn﹣2(n≥3)之间的关系式并计算a1 , a2 , a3;
(Ⅱ)猜想数列{an}的通项公式,并用数学归纳法加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.
成绩分组 | 频数 | 频率 |
(160,165] | 5 | 0.05 |
(165,170] | ① | 0.35 |
(170,175] | 30 | ② |
(175,180] | 20 | 0.20 |
(180,185] | 10 | 0.10 |
合计 | 100 | 1 |
(1)请先求出频率分布表中①、②位置相应的数据,再画出频率分布直方图;
(2)为了能选拔出最优秀的学生,该高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官的面试,求第四组至少有一名学生被考官A面试的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球队与其他6支篮球队依次进行6场比赛,每场均决出胜负,设这支篮球队与其他篮球队比赛中获胜的事件是独立的,并且获胜的概率均为 ![]() .
.
(1)求这支篮球队首次获胜前已经负了两场的概率;
(2)求这支篮球队在6场比赛中恰好获胜3场的概率;
(3)求这支篮球队在6场比赛中获胜场数的期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com