Question

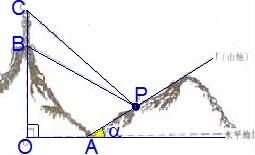
某人在一山坡P处观看对面山项上的一座铁塔，如图所示，塔及所在的山崖可视为图中的竖线OC，塔高BC?80（米），山高OB?220（米），OA?200（米），图中所示的山坡可视为直线l且点P在直线l上，l与水平地面的夹角为α，tanα=

1

2

．试问，此人距山崖的水平地面多高时，观看塔的视角∠BPC最大（不计此人的身高）？

Answer 1

分析：先建立直角坐标系，则依题意可知A，B，C的坐标，进而可得直线l的方程．设点P的坐标为（x，y）进而可求直线PC和PB的斜率，直线PC到直线PB的角的公式可得到tanBPC关于x的表达式tanBPC=

64

x+ 160×640 x -288

，要使tanBPC达到最大，只须x+

160×640

x

-288达到最小．再由均值不等式可知当且仅当x=

160×640

x

时上式取等号．故当x=320时tanBPC最大．进而得出此时点P的纵坐标，即可得到答案．

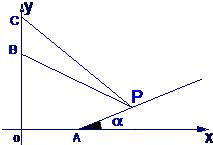解答：解：如图所示，建立平面直角坐标系，
则A（200，0），B（0，220），C（0，300）．
直线l的方程为y=（x-200）tanα，即y=

x-200

2

．
设点P的坐标为（x，y），则P(x，

x-200

2

)（x＞200）
由经过两点的直线的斜率公式kPC=

x-200 2 -300

x

=

x-800

2x

，kPB=

x-200 2 -220

x

=

x-640

2x

．
由直线PC到直线PB的角的公式得
tan∠BPC=

kPB-kPC

1+kPBkPC

=

160 2x

1+ x-800 2x • x-640 2x

=

64x

x2-288x+160×640

=

64

x+ 160×640 x -288

（x＞200）
要使tanBPC达到最大，只须x+

160×640

x

-288达到最小．
由均值不等式x+

160×640

x

-288≥2

160×640

-288．
当且仅当x=

160×640

x

时上式取等号．故当x=320时tanBPC最大．
这时，点P的纵坐标y为y=

320-200

2

=60．
由此实际问题知，0＜∠BPC＜

π

2

，
所以tanBPC最大时，∠BPC最大．
故当此人距水平地面60米高时，观看铁塔的视角∠BPC最大．

点评：本题主要考查解三角形的实际运用．有些问题需要建立直角坐标系，利用解析几何的方法来解决．