
【题目】在平面直角坐标系中,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 经过点
经过点![]() ,其中
,其中![]() 为椭圆
为椭圆![]() 的离心率.过点
的离心率.过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(
两点(![]() 在
在![]() 轴下方).
轴下方).
(1)求椭圆![]() 的方程;
的方程;
(2)过原点![]() 且平行于
且平行于![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() ,
, ![]() ,求
,求![]() 的值;
的值;
(3)记直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .若
.若![]() ,求直线
,求直线![]() 的斜率
的斜率![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)将点坐标代入椭圆方程,化简可得![]() (2)根据投影可得
(2)根据投影可得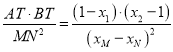 ,联立直线方程与椭圆方程,利用韦达定理代入化简可得定值(3)先求交点坐标,再根据
,联立直线方程与椭圆方程,利用韦达定理代入化简可得定值(3)先求交点坐标,再根据![]() ,得
,得![]() ,利用(2)韦达定理得等量关系,解出直线
,利用(2)韦达定理得等量关系,解出直线![]() 的斜率
的斜率![]() .
.
试题解析:(1)因为椭圆![]() 经过点
经过点![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
整理得![]() ,解得
,解得![]() 或
或![]() (舍),所以椭圆
(舍),所以椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
, ![]() .因为
.因为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .
.
联立直线![]() 与椭圆方程
与椭圆方程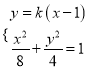 ,
,
消去![]() ,得
,得![]() ,所以
,所以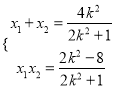 .
.
因为![]() ,所以直线
,所以直线![]() 方程为
方程为![]() ,
,
联立直线![]() 与椭圆方程
与椭圆方程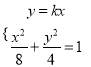 ,消去
,消去![]() 得
得![]() ,解得
,解得![]() .
.
因为![]() ,所以
,所以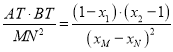 .
.
因为![]()
![]() ,
,
![]() ,
,
所以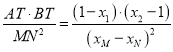
![]() .
.
(3)在![]() 中,令
中,令![]() ,则
,则![]() ,所以
,所以![]() ,
,
从而![]() ,
, ![]() .
.
因为![]() ,所以
,所以![]() ,即
,即![]() .
.
由(2)知, 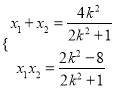 .
.
由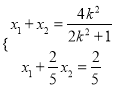 ,解得
,解得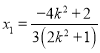 ,
, 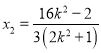 .
.
因为![]() ,所以
,所以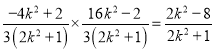 ,
,
整理得![]() ,解得
,解得![]() 或
或![]() (舍).
(舍).
又因为![]() ,所以
,所以![]() .
.


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:
【题目】双曲线![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 作倾斜角为
作倾斜角为![]() 的直线与
的直线与![]() 轴和双曲线的右支分别交于
轴和双曲线的右支分别交于![]() 两点,若点
两点,若点![]() 平分线段
平分线段![]() ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计,目前微信用户已达10亿,2016年,诸多传统企业大佬纷纷尝试进入微商渠道,让这个行业不断地走向正规化、规范化.2017年3月25日,第五届中国微商博览会在山东济南舜耕国际会展中心召开,力争为中国微商产业转型升级,某品牌饮料公司对微商销售情况进行中期调研,从某地区随机抽取6家微商一周的销售金额(单位:百元)的茎叶图如图所示,其中茎为十位数,叶为个位数.

(1)若销售金额(单位:万元)不低于平均值![]() 的微商定义为优秀微商,其余为非优秀微商,根据茎叶图推断该地区110家微商中有几家优秀?
的微商定义为优秀微商,其余为非优秀微商,根据茎叶图推断该地区110家微商中有几家优秀?
(2)从随机抽取的6家微商中再任取2家举行消费者回访调查活动,求恰有1家是优秀微商的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2018·赣中联考]李冶(1192-1279),真实栾城(今属河北石家庄市)人,金元时期的数学家、诗人,晚年在封龙山隐居讲学,数学著作多部,其中《益古演段》主要研究平面图形问题:求圆的直径、正方形的边长等.其中一问:现有正方形方田一块,内部有一个圆形水池,其中水池的边缘与方田四边之间的面积为13.75亩,若方田的四边到水池的最近距离均为二十步,则圆池直径和方田的边长分别是(注:240平方步为1亩,圆周率按3近似计算)( )
A. 10步,50步 B. 20步,60步 C. 30步,70步 D. 40步,80步
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“秃发”是一种常见的毛发疾病,随着发病人群年龄结构的年变化,逐渐引起了社会的广泛关注.一个人出生时头发数量约为100000根,数学徐老师建立了“秃发”函数模型作预估:一个人![]() 岁时的头发根数为
岁时的头发根数为![]() ,其中
,其中![]() 称为“脱发指数”.
称为“脱发指数”.
(1)杜老师5岁时有74375根头发,请依据模型求出杜老师的“脱发指数”![]() 的值;
的值;
(2)徐老师的学生认为“秃发”函数模型中有两个缺点:①头发的根数应该为整数;②头发的根数不能为负数,徐老师感觉很有道理,将模型作了两处修正,请写出修正后(1)问中杜老师的“秃发”函数模型,并求出杜老师几岁时头发最多.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产一种产品,根据经验,其次品率![]() 与日产量
与日产量![]() (万件)之间满足关系,
(万件)之间满足关系, (其中
(其中![]() 为常数,且
为常数,且![]() ,已知每生产1万件合格的产品以盈利2万元,但每生产1万件次品将亏损1万元(注:次品率=次品数/生产量, 如
,已知每生产1万件合格的产品以盈利2万元,但每生产1万件次品将亏损1万元(注:次品率=次品数/生产量, 如![]() 表示每生产10件产品,有1件次品,其余为合格品).
表示每生产10件产品,有1件次品,其余为合格品).
(1)试将生产这种产品每天的盈利额![]() (万元)表示为日产量
(万元)表示为日产量![]() (万件)的函数;
(万件)的函数;
(2)当日产量为多少时,可获得最大利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com