在等比数列{an}中,an>0 (n∈N*),公比q∈(0,1),且a1a5+2a3a5+a2a8=25,又a3与a5的等比中项为2.
(1)求数列{an}的通项公式
(2)设bn=log2an,求数列{|bn|}的前n项和Tn.
解:(1)∵{a
n} 为等比数列,∴
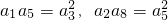
,
∴由题意得
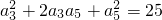
,
即
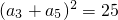
,∴a
3+a
5=±5,
又∵a
n>0,∴a
3+a
5>0,∴a
3+a
5=5,
又 与a
5 的等比中项为2.∴a
3a
5=4,
∴a
3=1,a
5=4 或a
3=4,a
5=1,
又∵q∈(0,1),∴a
3=4,a
5=1,
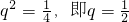
,
∴a
1=16,
∴
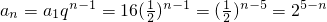
.
(2)b
n=log
2a
n=5-n,
∵b
n+1-b
n=-1,
∴{b
n} 是等差数列,则其前n 的和为

又∵当n≤5,n∈N
*时,b
n≥0;
当n>5,n∈N
*时,b
n<0,
∴当n≤5,n∈N
*时,T
n=|b
1|+|b
2|+|b
3|+…+|b
n|=b
1+b
2+b
3+…+b
n =

,
当n>5,n∈N
*时,T
n=|b
1|+|b
2|+|b
3|+…+|b
n|=b
1+b
2+b
3+b
4+b
5-b
6-b
7-…-b
n =S
5-(S
n-S
5)=2S
5-S
n =

∴T
n=

,n∈N
*.
分析:(1)将数列的已知条件利用等比数列的性质,用解方程组求出a
3,a
5,进而求出首项与公比,利用等比数列的通项公式求出数列{a
n}的通项公式.
(2)求出数列{b
n}的通项,利用等差数列的前n项和公式求出数列{b
n}的前n项和,进而通过b
n的正负来寻找T
n与S
n的关系.
点评:解决等比数列、等差数列两个特殊数列的有关问题,常利用它们的通项公式、前n项和公式列出方程组,通过解方程组求出通项和公差、公比再求其他量即可,属中档题.

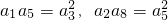 ,
,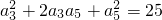 ,
,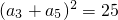 ,∴a3+a5=±5,
,∴a3+a5=±5,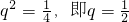 ,
,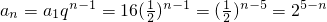 .
.
 ,
,
 ,n∈N*.
,n∈N*.

 阅读快车系列答案
阅读快车系列答案