已知向量$\overrightarrow{a}$=.$\overrightarrow{b}$=(x.y)．(Ⅰ)若x.y分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1.2.3.4.5.6)先后抛掷两次时.第1次.第2次出现的点数.求满足$\overrightarrow{a}$•$\overrightarrow{b}$=-1的概率,(Ⅱ)若x.y分别表示由计� 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

19．已知向量$\overrightarrow{a}$=（1，-2），$\overrightarrow{b}$=（x，y）．
（Ⅰ）若x，y分别表示将一枚质地均匀的正方体骰子（六个面的点数分别为1，2，3，4，5，6）先后抛掷两次时，第1次、第2次出现的点数，求满足$\overrightarrow{a}$•$\overrightarrow{b}$=-1的概率；
（Ⅱ）若x，y分别表示由计算机产生的两组1～6之间的均匀随机数，求满足$\overrightarrow{a}$•$\overrightarrow{b}$＞0的概率．

分析（Ⅰ）本小题考查的知识点是古典概型，关键是要找出满足条件满足$\overrightarrow{a}$•$\overrightarrow{b}$=-1的基本事件个数，及总的基本事件的个数，再代入古典概型公式进行计算求解．
（Ⅱ）本小题考查的知识点是几何概型的意义，关键是要画出满足条件的图形，结合图形分析，找出满足条件的点集对应的图形面积，及图形的总面积．

解答解：（Ⅰ）设（x，y）表示一个基本事件，则抛掷两次骰子的所有基本事件有：
（1，1），（1，2），（1，3），（1，4），（1，5），（1，6），
（2，1），（2，2），（2，3），（2，4），（2，5），（2，6），
（3，1），（3，2），（3，3），（3，4），（3，5），（3，6），
（4，1），（4，2），（4，3），（4，4），（4，5），（4，6），
（5，1），（5，2），（5，3），（5，4），（5，5），（5，6），
（6，1），（6，2），（6，3），（6，4），（6，5），（6，6），共36个．﹍﹍﹍﹍﹍﹍（3分）
用A表示事件“$\overrightarrow{a}$•$\overrightarrow{b}$=-1”，即x-2y=-1．
则A包含的基本事件有：（1，1），（3，2），（5，3），共3个．﹍﹍﹍﹍﹍﹍（5分）
∴P（A）=$\frac{3}{36}$=$\frac{1}{12}$．﹍﹍﹍﹍﹍﹍（7分）
（Ⅱ）用B表示事件“$\overrightarrow{a}$•$\overrightarrow{b}$＞0”，即x-2y＞0．
试验的全部结果所构成的区域为{（x，y）|1≤x≤6，1≤y≤6}，﹍﹍﹍﹍﹍﹍（9分）
构成事件B的区域为{（x，y）|1≤x≤6，1≤y≤6，x-2y＞0}，﹍﹍﹍﹍﹍﹍（12分）
如图所示

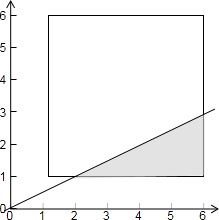
所以所求的概率为P（B）=$\frac{\frac{1}{2}×4×2}{5×5}$=$\frac{4}{25}$．﹍﹍﹍﹍﹍﹍（14分）

点评古典概型要求所有结果出现的可能性都相等，强调所有结果中每一结果出现的概率都相同．弄清一次试验的意义以及每个基本事件的含义是解决问题的前提，正确把握各个事件的相互关系是解决问题的关键．解决问题的步骤是：计算满足条件的基本事件个数，及基本事件的总个数，然后代入古典概型计算公式进行求解．
几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．解决的步骤均为：求出满足条件A的基本事件对应的“几何度量”N（A），再求出总的基本事件对应的“几何度量”N，最后根据P=$\frac{N（A）}{N}$求解．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>