【题目】已知集合
，则集合
各子集中元素之和为（ ）
A.320B.240C.160D.8
【答案】B
【解析】
由题意，分别计算出当集合
的子集中含有元素个数为0、1、2、3、4、5时，元素1、2、3、4、5出现的次数，进而可得元素1、2、3、4、5出现的总次数，即可得解.
当集合的子集为空集时，各元素之和为0；
当集合的子集含有1个元素时，共有
个集合，1、2、3、4、5各出现1次；
当集合的子集含有2个元素时，共有
个集合，1、2、3、4、5各出现4次；
当集合的子集含有3个元素时，共有
个集合，1、2、3、4、5各出现6次；
当集合的子集含有4个元素时，共有
个集合，1、2、3、4、5各出现4次；
当集合的子集含有5个元素时，共有
个集合，1、2、3、4、5各出现1次；
所以集合各子集中，1、2、3、4、5各出现了
次，
所以集合各子集中元素之和为
.
故选：B.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
【题目】（1）已知两个变量线性相关，若它们的相关性越强，则相关系数的绝对值越接近于1.
（2）线性回归直线必过点
；
（3）对于分类变量A与B的随机变量
，越大说明“A与B有关系”的可信度越大.
（4）在刻画回归模型的拟合效果时，残差平方和越小，相关指数
的值越大，说明拟合的效果越好.
（5）根据最小二乘法由一组样本点
，求得的回归方程是
，对所有的解释变量
,
的值一定与
有误差.
以上命题正确的序号为____________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图是某直三棱柱被削去上底后所得几何体的左视图、俯视图、直观图，在直观图中，M是BD的中点，左视图是直角梯形，俯视图是等腰直角三角形，有关数据如图所示.
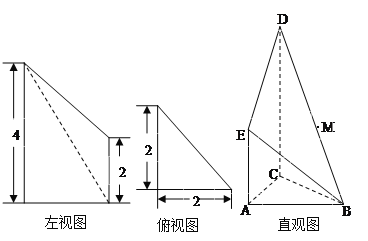
（Ⅰ）求该几何体的表面积和体积；
（Ⅱ）求点C到平面MAB的距离.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在一个十进制正整数中，如果它含有偶数（包括零）个数字 8 ，则称它为“优数” ，否则就称它为“非优数” .那么，长度（位数）不超过
（是正整数）的所有“优数” 的个数是 __________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某学校共有教师300人，其中中级教师有120人，高级教师与初级教师的人数比为
.为了解教师专业发展要求，现采用分层抽样的方法进行调查，在抽取的样本中有中级教师72人，则该样本中的高级教师人数为__________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某书店刚刚上市了《中国古代数学史》，销售前该书店拟定了5种单价进行试销，每种单价（
元）试销l天，得到如表单价（元）与销量
（册）数据：
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
（l）根据表中数据，请建立关于的回归直线方程：
（2）预计今后的销售中，销量（册）与单价（元）服从（l）中的回归方程，已知每册书的成本是12元，书店为了获得最大利润，该册书的单价应定为多少元？
附：
，
，
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某家庭进行理财投资，根据长期收益率市场预测，投资债券等稳健型产品的收益
与投资额
成正比，且投资1万元时的收益为
万元，投资股票等风险型产品的收益
与投资额的算术平方根成正比，且投资1万元时的收益为0.5万元，
（1）分别写出两种产品的收益与投资额的函数关系；
（2）该家庭现有20万元资金，全部用于理财投资，问：怎样分配资金能使投资获得最大收益，其最大收益为多少万元？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲乙两地的高速公路全长166千米，汽车从甲地进入该高速公路后匀速行驶到乙地，车速
（千米/时）.已知汽车每小时的运输成本（以元为单位）由可变部分和固定部分组成：可变部分为
，固定部分为220元.
(1)把全程运输成本
（元）表示为速度
（千米/时）的函数，并指出这个函数的定义域；
(2)汽车应以多大速度行驶才能使全程运输成本最小？最小运输成本为多少元？（结果保留整数）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
