
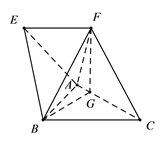
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 为梯形,
为梯形, ![]() ,且
,且![]() ,
, ![]() 是边长为2的正三角形,顶点
是边长为2的正三角形,顶点![]() 在
在![]() 上的射影为点
上的射影为点![]() ,且
,且![]() ,
, ![]() ,
, ![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1) 取![]() 的中点为
的中点为![]() ,连接
,连接![]() 利用直角三角形的性质,可分别求出
利用直角三角形的性质,可分别求出![]() 的值,由勾股定理得
的值,由勾股定理得![]() .可得
.可得![]() 面
面![]() ,可证平面
,可证平面![]() 平面
平面![]() ;(2)以
;(2)以![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 所在直线为
所在直线为![]() 轴,过点
轴,过点![]() 作平面
作平面![]() 的垂线为
的垂线为![]() 轴,建立空间直角坐标系,写出各点坐标,求出两个半平面的法向量,利用法向量的夹角与二面角的夹角的关系,可求二面角的余弦值.
轴,建立空间直角坐标系,写出各点坐标,求出两个半平面的法向量,利用法向量的夹角与二面角的夹角的关系,可求二面角的余弦值.
试题解析:(Ⅰ)证明:由顶点![]() 在
在![]() 上投影为点
上投影为点![]() ,可知,
,可知, ![]() .
.
取![]() 的中点为
的中点为![]() ,连结
,连结![]() ,
, ![]() .
.
在![]() 中,
中, ![]() ,
, ![]() ,所以
,所以![]() .
.
在![]() 中,
中, ![]() ,
, ![]() ,所以
,所以![]() .
.
所以, ![]() ,即
,即![]() .
.
∵ ![]()
∴![]() 面
面![]() .
.
又![]() 面
面![]() ,所以面
,所以面![]() 面
面![]() .
.
(Ⅱ)由(Ⅰ)知, ![]() ,
, ![]() ,且
,且![]()
所以 ![]() 面
面![]() ,且
,且![]() 面
面![]() .以
.以![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 所在直线为
所在直线为![]() 轴,过点
轴,过点![]() 作平面
作平面![]() 的垂线为
的垂线为![]() 轴,建立空间直角坐标系,如图所示:
轴,建立空间直角坐标系,如图所示:

![]() ,
, ![]() ,
, ![]() ,
,

设平面![]() ,
, ![]() 的法向量分别为
的法向量分别为![]() ,则
,则
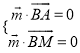 ,则
,则![]() ,
,
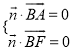 ,则
,则
![]() ,
,
 ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)若曲线![]() 与曲线
与曲线![]() 在它们的交点
在它们的交点![]() 处具有公共切线,求a,b的值;
处具有公共切线,求a,b的值;
(2)当![]() 时,若函数
时,若函数![]() 在区间
在区间![]() 内恰有两个零点,求a的取值范围;
内恰有两个零点,求a的取值范围;
(3)![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知函数f(x)=![]() -bx+lnx(a,b∈R).
-bx+lnx(a,b∈R).
(Ⅰ)若a=b=1,求f(x)点(1,f(1))处的切线方程;
(Ⅱ)设a<0,求f(x)的单调区间;
(Ⅲ)设a<0,且对任意的x>0,f(x)≤f(2),试比较ln(-a)与-2b的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市的甲区、乙区分别对6个企业进行评估,综合得分情况如茎叶图所示.
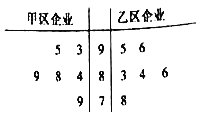
(1)根据茎叶图,分别求甲、乙两区引进企业得分的平均值;
(2)规定85分以上(含85分)为优秀企业,若从甲、乙两个区准备引进的优秀企业中各随机选取一个,求这两个企业得分的差的绝对值不超过5分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了改善居民的休闲娱乐活动场所,现有一块矩形![]() 草坪如下图所示,已知:
草坪如下图所示,已知:![]() 米,
米,![]() 米,拟在这块草坪内铺设三条小路
米,拟在这块草坪内铺设三条小路![]() 、
、![]() 和
和![]() ,要求点
,要求点![]() 是
是![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 时上,且
时上,且![]() .
.

(1)设![]() ,试求
,试求![]() 的周长
的周长![]() 关于
关于![]() 的函数解析式,并求出此函数的定义域;
的函数解析式,并求出此函数的定义域;
(2)经核算,三条路每米铺设费用均为![]() 元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.
元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①命题“![]() ,有
,有![]() ”的否定为:“
”的否定为:“![]()
![]() ”;
”;
②已知向量![]() 与
与![]() 的夹角是钝角,则实数k的取值范围是
的夹角是钝角,则实数k的取值范围是![]() ;
;
③函数![]() 的单调递增区间是
的单调递增区间是![]() ;
;
④“![]() ”是“直线
”是“直线![]() 和直线
和直线![]() 平行”的充分不必要条件;
平行”的充分不必要条件;
其中错误命题的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四棱柱![]() 的底面边长为2,侧棱
的底面边长为2,侧棱![]() ,
,![]() 为上底面
为上底面![]() 上的动点,给出下列四个结论中正确结论为( )
上的动点,给出下列四个结论中正确结论为( )
A.若![]() ,则满足条件的
,则满足条件的![]() 点有且只有一个
点有且只有一个
B.若![]() ,则点
,则点![]() 的轨迹是一段圆弧
的轨迹是一段圆弧
C.若![]() ∥平面
∥平面![]() ,则
,则![]() 长的最小值为2
长的最小值为2
D.若![]() ∥平面
∥平面![]() ,且
,且![]() ,则平面
,则平面![]() 截正四棱柱
截正四棱柱![]() 的外接球所得平面图形的面积为
的外接球所得平面图形的面积为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A4纸是生活中最常用的纸规格.A系列的纸张规格特色在于:①A0、A1、A2…、A5,所有尺寸的纸张长宽比都相同.②在A系列纸中,前一个序号的纸张以两条长边中点连线为折线对折裁剪分开后,可以得到两张后面序号大小的纸,比如1张A0纸对裁后可以得到2张A1纸,1张A1纸对裁可以得到2张A2纸,依此类推.这是因为A系列纸张的长宽比为![]() :1这一特殊比例,所以具备这种特性.已知A0纸规格为84.1厘米×118.9厘米.118.9÷84.1≈1.41≈
:1这一特殊比例,所以具备这种特性.已知A0纸规格为84.1厘米×118.9厘米.118.9÷84.1≈1.41≈![]() ,那么A4纸的长度为( )
,那么A4纸的长度为( )
A.![]() 厘米B.
厘米B.![]() 厘米C.
厘米C.![]() 厘米D.
厘米D.![]() 厘米
厘米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com