
已知关于 的不等式
的不等式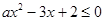 的解集为
的解集为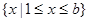 .
.
(1)求实数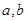 的值;
的值;
(2)解关于 的不等式:
的不等式: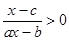 (
(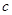 为常数).
为常数).
(1)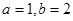 ;(2)当
;(2)当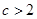 时解集为
时解集为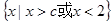 ; 当
; 当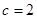 时解集为
时解集为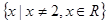 ;
;
当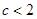 时解集为
时解集为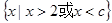 .
.
解析试题分析:(1)三个二次间的关系,其实质是抓住二次函数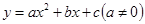 的图像与横坐标的交点、二次不等式
的图像与横坐标的交点、二次不等式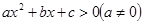 解集的端点值、二次方程
解集的端点值、二次方程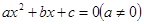 的根是同一个问题.解决与之相关的问题时,可利用函数与方程的思想、化归的思想将问题转化,结合二次函数的图象来解决;(2)把分式不等式转化成整式不等式,注意看清分子、分母的符号;(3)解含参数的一元二次不等式分类讨论的依据:一是二次项中若含有参数应讨论是小于0,等于0,还是大于0,然后将不等式转化为二次项系数为正的形式,二是当不等式对应的方程的根个数不确定时,讨论判别式
的根是同一个问题.解决与之相关的问题时,可利用函数与方程的思想、化归的思想将问题转化,结合二次函数的图象来解决;(2)把分式不等式转化成整式不等式,注意看清分子、分母的符号;(3)解含参数的一元二次不等式分类讨论的依据:一是二次项中若含有参数应讨论是小于0,等于0,还是大于0,然后将不等式转化为二次项系数为正的形式,二是当不等式对应的方程的根个数不确定时,讨论判别式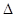 与0的关系,三是确定无根时可直接写出解集,确定方程有两个根时,要讨论两根的大小关系,从而确定解集;(4)讨论时注意找临界条件.
与0的关系,三是确定无根时可直接写出解集,确定方程有两个根时,要讨论两根的大小关系,从而确定解集;(4)讨论时注意找临界条件.
试题解析:解:(1)由题知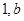 为关于
为关于 的方程
的方程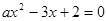 的两根,
的两根,
即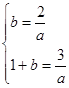 ∴
∴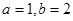 . 3分
. 3分
(2)不等式等价于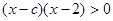 ,
,
所以:当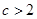 时解集为
时解集为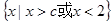 ;
;
当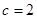 时解集为
时解集为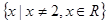 ;
;
当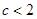 时解集为
时解集为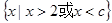 . 6分
. 6分
考点:(1)一元二次不等式的应用;(2)解分式不等式.


科目:高中数学 来源: 题型:解答题
设二次函数f(x)=ax2+bx+c,函数F(x)=f(x)-x的两个零点为m,n(m<n).
(1)若m=-1,n=2,求不等式F(x)>0的解集;
(2)若a>0,且0<x<m<n<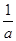 ,比较f(x)与m的大小.
,比较f(x)与m的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com