
分析 (1)由可推知f(-x)=f(x),从而可判断函数f(x)的奇偶性;
(2)利用(1)知f(x)为偶函数,可知当x∈(0,+∞)时,x3>0,从而可判知,要使f(x)+f(2x)>0在其定义域上恒成立,只需当a>1时即可.
解答 解:(1)定义域为(-∞,0)∪(0,+∞),
∵f(-x)=($\frac{1}{{a}^{-x}-1}$+$\frac{1}{2}$)(-x)3=-($\frac{{a}^{x}}{1-{a}^{2}}$+$\frac{1}{2}$)x3=($\frac{1}{{a}^{x}-1}$+$\frac{1}{2}$)=f(x)
∴f(x)是偶函数.
(2)∵函数f(x)在定义域上是偶函数,
∴函数y=f(2x)在定义域上也是偶函数,
∴当x∈(0,+∞)时,f(x)+f(2x)>0可满足题意,
∵当x∈(0,+∞)时,x3>0,
∴只需$\frac{1}{{a}^{x}-1}$+$\frac{1}{2}$+$\frac{1}{({a}^{x})^{2}-1}$+$\frac{1}{2}$>0,即$\frac{{a}^{2x}+{a}^{x}+1}{{a}^{2x}-1}$>0,
∵a2x+ax+1>0,
∴(ax)2-1>0,解得a>1,
∴当a>1时,f(x)+f(2x)>0在定义域上恒成立.
点评 本题考查函数恒成立问题,考查函数单调性的判断与证明,考查函数奇偶性的运用,突出转化思想与分析法的应用,属于中档题.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:解答题
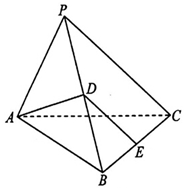 在三棱锥P-ABC中,AP=AB,平面PAB⊥平面ABC,∠ABC=90°,D,E分别为PB,BC的中点.
在三棱锥P-ABC中,AP=AB,平面PAB⊥平面ABC,∠ABC=90°,D,E分别为PB,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
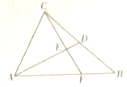 如图△ABC,点D是BC中点,$\overrightarrow{AF}$=2$\overrightarrow{FB}$,CF和AD交于点E,设$\overrightarrow{AD}$=a,$\overrightarrow{AB}$=b.
如图△ABC,点D是BC中点,$\overrightarrow{AF}$=2$\overrightarrow{FB}$,CF和AD交于点E,设$\overrightarrow{AD}$=a,$\overrightarrow{AB}$=b.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-[x]≥0 | |
| B. | x-[x]<1 | |
| C. | 令f(x)=x-[x],对任意实数x,f(x+1)=f(x)恒成立 | |
| D. | 令f(x)=x-[x],对任意实数x,f(-x)=f(x)恒成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x${\;}^{\frac{1}{3}}$ | B. | f(x)=sinx | C. | f(x)=cosx | D. | f(x)=log2(x2+1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com