[题目]已知函数f(x)=(log2x)2﹣4log2x+1．的值,的最大值和最小值．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知函数f（x）=（log2x）2﹣4log2x+1．
（1）求f（8）的值；
（2）当2≤x≤16时，求f（x）的最大值和最小值．

【答案】
（1）解：∵函数，

∴f（8）= =9﹣4×3+1=﹣2

（2）解：当2≤x≤16时，1≤log2x≤4．令 t=log2x，则1≤t≤4，f（x）=t2﹣4t+1=（t﹣2）2﹣3，

故当t=2时，f（x）取得最小值为﹣3，当t=4时，f（x）取得最大值为 1

【解析】（1）根据函数的解析式可得f（8）= ，再利用对数的运算性质，求出结果．（2）当2≤x≤16时，令 t=log2x，则1≤t≤4，f（x）=t2﹣4t+1=（t﹣2）2﹣3，根据二次函数的性质求出f（x）的最大值和最小值．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知各项均为整数的数列{an}满足an2≤1，1≤a12+a22+…+an2≤m，m，n∈N* ．
（1）若m=1，n=2，写出所有满足条件的数列{an}；
（2）设满足条件的{an}的个数为f（n，m）．
①求f（2，2）和f（2016，2016）；
②若f（m+1，m）＞2016，试求m的最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某险种的基本保费为（单位：元），继续购买该险种的投保人称为续保人，

续保人本年度的保费与其上年度出险次数的关联如下：

上年度出险次数	0	1	2	3	4
保费

随机调查了该险种的400名续保人在一年内的出险情况，得到如下统计表：

出险次数	0	1	2	3	4
频数	120	100	60	60	40	20

（Ⅰ）记A为事件：“一续保人本年度的保费不高于基本保费”.求的估计值；

（Ⅱ）记B为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的190％”.

求的估计值；

（III）求续保人本年度的平均保费估计值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=
（1）求函数f（x）的零点；
（2）若实数t满足f（log2t）+f（log2 ）＜2f（2），求f（t）的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】“累积净化量”是空气净化器质量的一个重要衡量指标，它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量，以克表示，根据《空气净化器》国家标准，对空气净化器的累计净化量有如下等级划分：

累积净化量（克）				12以上
等级

为了了解一批空气净化器（共5000台）的质量，随机抽取台机器作为样本进行估计，已知这台机器的累积净化量都分布在区间中，按照、、、、均匀分组，其中累积净化量在的所有数据有：4.5,4.6,5.2,5.3,5.7和5.9，并绘制了频率分布直方图，如图所示：

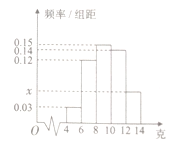
（1）求的值及频率分布直方图中的值；

（2）以样本估计总体，试估计这批空气净化器（共5000台）中等级为的空气净化器有多少台？

（3）从累积净化量在的样本中随机抽取2台，求恰好有1台等级为的概率.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】解答
（1）集合M={1，2，（m2﹣3m﹣1）+（m2﹣5m﹣6）i}，N={3，﹣1}，M∩N={3}，求实数m的值．
（2）已知12= ×1×2×3，12+22= ×2×3×5，12+22+32= ×3×4×7，12+22+32+42= ×4×5×9，由此猜想12+22+…+n2（n∈N*）的表达式并用数学归纳法证明．