B
分析:根据题中的条件acosA+bcosB=ccosC和三角形的内角和公式,利用三角函数的和(差)角公式和诱导公式得到2cosAcosB=0,得到A或B为

得到答案即可.
解答:∵acosA+bcosB=ccosC,
∴sinAcosA+sinBcosB=sinCcosC
∴sin2A+sin2B=sin2C,2sin(A+B)cos(A-B)=2sinCcosC
∴cos(A-B)=-cos(A+B),2cosAcosB=0
∴cosA=0或cosB=0,得
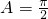
或

∴△ABC是直角三角形.
故答案为B.
点评:考查学生三角函数中的恒等变换应用的能力.要灵活运用三角函数的和(差)角公式和诱导公式.

 得到答案即可.
得到答案即可.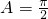 或
或

