
分析 (1)由已知条件利用焦点在x轴上的椭圆的性质,能求出m的取值范围.
(2)由已知条件利用焦点在y轴上的椭圆的性质,能求出m的取值范围.
解答 解:(1)∵方程$\frac{{x}^{2}}{5m-6}$+$\frac{{y}^{2}}{m+2}$=1表示焦点在x轴上的椭圆,
∴$\left\{\begin{array}{l}{5m-6>0}\\{m+2>0}\\{5m-6>m+2}\end{array}\right.$,
解得m>2,
∴m的取值范围是(2,+∞).
(2)∵方程$\frac{{x}^{2}}{5m-6}$+$\frac{{y}^{2}}{m+2}$=1表示焦点在y轴上的椭圆,
∴$\left\{\begin{array}{l}{5m-6>0}\\{m+2>0}\\{5m-6<m+2}\end{array}\right.$,
解得$\frac{6}{5}<m<2$.
∴m的取值范围是($\frac{6}{5}$,2).
点评 本题考查满足条件的实数的取值范围的求法,是基础题,解题时要认真审题,注意椭圆的性质的合理运用.


科目:高中数学 来源: 题型:填空题
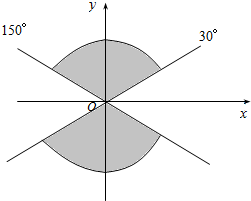 已知角α的终边在图中阴影部分所表示的范围内(不包括边界),则α的取值范围为{α|k•180°+30°<α<k•180°+150°,k∈Z}.
已知角α的终边在图中阴影部分所表示的范围内(不包括边界),则α的取值范围为{α|k•180°+30°<α<k•180°+150°,k∈Z}.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 家庭类型 | 贫困 | 温饱 | 小康 | 富裕 |
| n | n≥59% | 50%≤n<59% | 40%≤n<50% | 30%≤n<40% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$+$\frac{\sqrt{3}}{4}$ | B. | $\frac{1}{2}$-$\frac{\sqrt{3}}{4}$ | C. | $\frac{3}{4}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪(2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-2,0)∪(2,+∞) | D. | (-2,0)∪(0,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com