
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 的准线与
的准线与![]() 轴的交点为
轴的交点为![]() ,点
,点![]() 是
是![]() 上的动点.当
上的动点.当![]() 是等腰直角三角形时,其面积为2.
是等腰直角三角形时,其面积为2.
(1)求![]() 的方程;
的方程;
(2)延长AF交C于点B,点M是C的准线上的一点,设直线![]() ,
,![]() ,
,![]() 的斜率分别是
的斜率分别是![]() ,证明:
,证明:![]() .
.
科目:高中数学 来源: 题型:
【题目】已知直线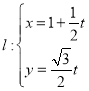 (
(![]() 为参数),曲线
为参数),曲线![]() (
(![]() 为参数).
为参数).
(1)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求劣弧
两点,求劣弧![]() 的弧长;
的弧长;
(2)若把曲线![]() 上各点的横坐标缩短为原来的
上各点的横坐标缩短为原来的![]() ,纵坐标缩短为原来的
,纵坐标缩短为原来的![]() ,得到曲线
,得到曲线![]() ,设点
,设点![]() 是曲线
是曲线![]() 上的一个动点,求点
上的一个动点,求点![]() 到直线
到直线![]() 的距离的最小值,及点
的距离的最小值,及点![]() 坐标.
坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() (
(![]() 为参数,实数
为参数,实数![]() ),曲线
),曲线![]() :
:![]() (
(![]() 为参数,实数
为参数,实数![]() ).在以
).在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() (
(![]() ,
,![]() )与
)与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点,当
两点,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】武汉又称江城,是湖北省省会城市,被誉为中部地区中心城市,它不仅有着深厚的历史积淀与丰富的民俗文化,更有着众多名胜古迹与旅游景点,每年来武汉参观旅游的人数不胜数,其中黄鹤楼与东湖被称为两张名片为合理配置旅游资源,现对已游览黄鹤楼景点的游客进行随机问卷调查,若不游玩东湖记1分,若继续游玩东湖记2分,每位游客选择是否游览东湖景点的概率均为![]() ,游客之间选择意愿相互独立.
,游客之间选择意愿相互独立.
(1)从游客中随机抽取3人,记总得分为随机变量![]() ,求
,求![]() 的分布列与数学期望;
的分布列与数学期望;
(2)(i)若从游客中随机抽取![]() 人,记总分恰为
人,记总分恰为![]() 分的概率为
分的概率为![]() ,求数列
,求数列![]() 的前10项和;
的前10项和;
(ⅱ)在对所有游客进行随机问卷调查过程中,记已调查过的累计得分恰为![]() 分的概率为
分的概率为![]() ,探讨
,探讨![]() 与
与![]() 之间的关系,并求数列
之间的关系,并求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 |
|
|
|
|
|
|
设该险种一续保人一年内出险次数与相应概率如下:
一年内出险次数 | 0 | 1 | 2 | 3 | 4 |
|
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
(1)求一续保人本年度的保费高于基本保费的概率;
(2)已知一续保人本年度的保费高于基本保费,求其保费比基本保费高出![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com