Question

16．棱长为a的正方体ABCD-A₁B₁C₁D₁中，与D₁B平行的平面截正方体所得截面面积为S，则S的取值范围是（　　）

• A． （ 0，$\frac{\sqrt{6}{a}^{2}}{2}$）
• B． （0，$\frac{3\sqrt{3}{a}^{2}}{4}$]
• C． （0，$\frac{5{a}^{2}}{4}$）
• D． （0，$\frac{\sqrt{6}{a}^{2}}{4}$]

Answer 1

分析 根据题意，取AA₁与CC₁的中点M和N，得出四边形MBND₁的面积${S}_{四边形MB{ND}_{1}}$，
从而得出与D₁B平行的平面截正方体所得截面面积S的取值范围．

解答 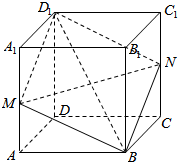解：根据题意，取AA₁的中点M，CC₁的中点N，
连接D₁M、MB、BN、ND₁，如图所示；
则MN⊥BD₁，
又AB=a，∴MN=$\sqrt{2}$a，BD₁=$\sqrt{3}$a，
∴四边形MBND₁的面积为${S}_{四边形MB{ND}_{1}}$=$\frac{1}{2}$•MN•BD₁=$\frac{1}{2}$×$\sqrt{2}$a×$\sqrt{3}$a=$\frac{\sqrt{6}}{2}$a²；
∴与D₁B平行的平面截正方体所得截面面积S的取值范围是（0，$\frac{\sqrt{6}}{2}$a²）．
故选：A．

点评 本题考查了空间中的位置关系的应用问题，也考查了转化思想的应用问题，是综合性题目．