
【题目】已知函数![]() 常数
常数![]() .
.
![]() 证明
证明![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数;
上是增函数;
![]() 当
当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
![]() 对于
对于![]() 中的函数
中的函数![]() 和函数
和函数![]() ,若对任意
,若对任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求实数a的值.
成立,求实数a的值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设△ABC的内角A、B、C所对边的长分别为a、b、c,且有2sinBcosA=sinAcosC+cosAsinC. (Ⅰ)求角A的大小;
(Ⅱ)若b=2,c=1,D为BC的中点,求AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在冬季,由于受到低温和霜冻的影响,蔬菜的价格会随着需求量的增加而提升.已知某供应商向饭店定期供应某种蔬菜,其价格会随着日需求量的增加而上升,具体情形统计如下表所示:

(1)根据上表中的数据进行判断,![]() 与
与![]() 哪一个更适合作为日供应量
哪一个更适合作为日供应量![]() 与单价
与单价![]() 之间的回归方程;(给出判断即可,不必说明理由);
之间的回归方程;(给出判断即可,不必说明理由);
(2)根据(1)的判断结果以及参考数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)该地区有![]() 个酒店,其中
个酒店,其中![]() 个酒店每日对蔬菜的需求量在
个酒店每日对蔬菜的需求量在![]() 以下,
以下,![]() 个酒店对蔬菜的需求量在
个酒店对蔬菜的需求量在![]() 以上,从这
以上,从这![]() 个酒店中任取
个酒店中任取![]() 个进行调查,求恰有
个进行调查,求恰有![]() 个酒店对蔬菜需求量在
个酒店对蔬菜需求量在![]() 以上的概率.
以上的概率.
参考公式及数据:
对于一组数据![]() ,
,![]() ...
...![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为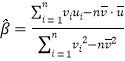 ,
,![]()

其中:![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数
上是增函数![]() 若函数
若函数![]() ,利用上述性质,
,利用上述性质,
![]() Ⅰ
Ⅰ![]() 当
当![]() 时,求
时,求![]() 的单调递增区间
的单调递增区间![]() 只需判定单调区间,不需要证明
只需判定单调区间,不需要证明![]() ;
;
![]() Ⅱ
Ⅱ![]() 设
设![]() 在区间
在区间![]() 上最大值为
上最大值为![]() ,求
,求![]() 的解析式;
的解析式;
![]() Ⅲ
Ⅲ![]() 若方程
若方程![]() 恰有四解,求实数a的取值范围.
恰有四解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为常数,
为常数, ![]() ,函数
,函数![]() ,
,![]() 且方程
且方程![]() 有等
有等
根.
(1)求![]() 的解析式及值域;
的解析式及值域;
(2)设集合![]() ,
,![]() ,若
,若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)是否存在实数![]() ,使
,使![]() 的定义域和值域分别为
的定义域和值域分别为![]() 和
和![]() ?若存在,求
?若存在,求
出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为加快新能源汽车产业发展,推进节能减排,国家对消费者购买新能源汽车给予补贴,其中对纯电动乘用车补贴标准如下表:
新能源汽车补贴标准 | |||
车辆类型 | 续驶里程R(公里) | ||
80≤R<150 | 150≤R<250 | R≥250 | |
纯电动乘用车 | 3.5万元/辆 | 5万元/辆 | 6万元/辆 |
某校研究性学习小组,从汽车市场上随机选取了M辆纯电动乘用车,根据其续驶里程R(单次充电后能行驶的最大里程)作出了频率与频数的统计表:
分组 | 频数 | 频率 |
80≤R<150 | 2 | 0.2 |
150≤R<250 | 5 | x |
R≥250 | y | z |
合计 | M | 1 |
(Ⅰ)求x,y,z,M的值;
(Ⅱ)若从这M辆纯电动乘用车中任选2辆,求选到的2辆车续驶里程都不低于150公里的概率;
(Ⅲ)若以频率作为概率,设X为购买一辆纯电动乘用车获得的补贴,求X的分布列和数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
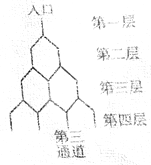
【题目】如图是在竖直平面内的一个“通道游戏”,图中竖直线段和斜线段都表示通道,并且在交点处相通,假设一个小弹子在交点处向左或向右是等可能的.若竖直线段有一条的为第一层,有两条的为第二层,……,依此类推,现有一颗小弹子从第一层的通道里向下运动.则该小弹子落入第四层从左向右数第3个竖直通道的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 曲线
曲线![]() 在原点处的切线为
在原点处的切线为![]() .
.
(1)证明:曲线![]() 与
与![]() 轴正半轴有交点;
轴正半轴有交点;
(2)设曲线![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,曲线在点
,曲线在点![]() 处的切线为直线
处的切线为直线![]() ,求证:曲线
,求证:曲线![]() 上的点都不在直线
上的点都不在直线![]() 的上方 ;
的上方 ;
(3)若关于![]() 的方程
的方程![]() (
(![]() 为正实数)有不等实根
为正实数)有不等实根![]() 求证:
求证:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com