
| A. | <b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
分析 根据题意,由函数的奇偶性分析可得f(-x)=f(x),则有2|x-m|-1=2|-x-m|-1,解可得m的值,即可得f(x)=2|x|-1,由此计算可得a、b、c的值,比较可得答案.
解答 解:根据题意,函数f(x)=2|x-m|-1为偶函数,
即f(-x)=f(x),则有2|x-m|-1=2|-x-m|-1,
解可得:m=0,
即f(x)=2|x|-1,
所以$a=f({{{log}_2}\frac{1}{3}})={2^{|{{{log}_2}\frac{1}{3}}|}}-1={2^{{{log}_2}3}}-1=3-1=2$,
$b=f({{{log}_2}5})={2^{{{log}_2}5}}-1=4,c=f({2m})=f(0)={2^0}-1=0$,
所以c<a<b,
故选C.
点评 本题考查函数的奇偶性的应用,涉及对数的计算,关键是利用函数的奇偶性的性质求出m的值.


科目:高中数学 来源: 题型:选择题
| A. | {3,5} | B. | {2,3,5} | C. | {2,5} | D. | {2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≤2 | B. | a≤1 | C. | a≤-1 | D. | a≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
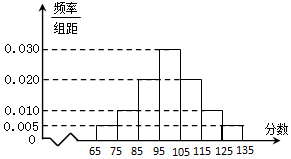 某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图:
某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com