
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
分析 由已知可得函数为定义域内的奇函数,并求得函数周期,把log220利用对数的运算性质转化为(-1,0)内的函数值求解.
解答 解:由f(-x)+f(x)=0,可知函数f(x)为定义域内的奇函数,
由f(x)=-f(x+2),得f(x+2)=-f(x),
∴f[(x+2)+2]=-f(x+2)=-[-f(x)]=f(x),
即f(4+x)=f(x),
∴f(x)是以4为周期的周期函数.
又x∈(-1,0)时,f(x)=2x-$\frac{1}{5}$,
∴f(log220)=f(-4+log220)=f($lo{g}_{2}\frac{20}{16}$)
=f($lo{g}_{2}\frac{5}{4}$)=-f($lo{g}_{2}\frac{4}{5}$)=-${2}^{lo{g}_{2}\frac{4}{5}}+\frac{1}{5}$=$-\frac{4}{5}+\frac{1}{5}=-\frac{3}{5}$.
故选:B.
点评 本题考查函数的周期性与奇偶性的性质,训练了与抽象函数有关的函数性质的应用,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 3 | C. | 6$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
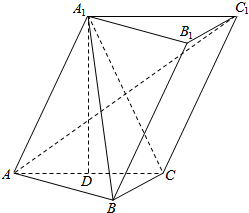 已知三棱柱ABC-A1B1C1,A1在底面ABC上的射影恰为AC的中点D,∠BCA=90°,AC=BC=2,又知BA1⊥AC1
已知三棱柱ABC-A1B1C1,A1在底面ABC上的射影恰为AC的中点D,∠BCA=90°,AC=BC=2,又知BA1⊥AC1查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x<2} | B. | {x|-1<x<1} | C. | {x|-1<x<2} | D. | {x|1≤x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 13 | D. | -$\frac{5}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com