
����Ŀ��Ϊ�˽�һ��ֲ���ʵ������������ȡһ����ֲ���ʵ������������(��λ����)������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��Ϊ5�飬��Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
��Ϊ5�飬��Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
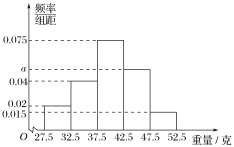
��1����ͼ��![]() ��ֵ��
��ֵ��
��2����������ֲ���ʵ������ƽ����![]() �ͷ���
�ͷ���![]() (ͬһ���е������ø���������е�ֵ������)��
(ͬһ���е������ø���������е�ֵ������)��
��3����֪����ֲ���ʵ����������32.5�˵ļ�Ϊ���ʹ�ʵ���������������壮��������ֲ���ʵ�������ȡ3�����������ʹ�ʵ�ĸ���Ϊ![]() ����
����![]() �ķֲ��к���ѧ����
�ķֲ��к���ѧ����![]() ��
��
 ��������������������ϵ�д�
��������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�ֱ��l�IJ�������Ϊ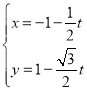 ��tΪ��������ֱ��l������C����y��1��2��x2��1����A��B���㣮
��tΪ��������ֱ��l������C����y��1��2��x2��1����A��B���㣮
��1����|AB|�ij���
��2������OΪ���㣬x���������Ϊ���Ὠ���ļ�����ϵ�У����P�ļ�����Ϊ![]() �����P���߶�AB�е�M�ľ��룮
�����P���߶�AB�е�M�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ![]() �У�����
�У�����![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() Ϊ�������������任
Ϊ�������������任 ������
������![]() �任Ϊ����
�任Ϊ����![]() .
.
��1������![]() Ϊ���㣬
Ϊ���㣬![]() ��ķǸ�����Ϊ���ᣨ��λ������ֱ������ϵ��ͬ���ļ�����ϵ�У���
��ķǸ�����Ϊ���ᣨ��λ������ֱ������ϵ��ͬ���ļ�����ϵ�У���![]() �ļ����귽�̣�
�ļ����귽�̣�
��2����֤��ֱ��![]() ������
������![]() �Ľ���Ҳ������
�Ľ���Ҳ������![]() ��.
��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ȳ�����![]() ��ǰn���ΪSn����
��ǰn���ΪSn����![]() Ϊ�Ȳ����У���
Ϊ�Ȳ����У���![]() ��
��
��1��������![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2���Ƿ����������![]() �� ʹ
�� ʹ![]() �ɵȱ����У������ڣ����������ȱ����У��������ڣ���˵�����ɣ�
�ɵȱ����У������ڣ����������ȱ����У��������ڣ���˵�����ɣ�
��3��������![]() ����
����![]() ��
��![]() ���Ҷ������
���Ҷ������![]() ������
������![]() ����������k����Сֵ��
����������k����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪{an}�ǵȲ����У�{bn}�Ǹ����Ϊ�����ĵȱ����У���b1��a1��1��b3��a4��b1��b2��b3��a3��a4.
(1)������{an}��{bn}��ͨ�ʽ��
(2)��cn��anbn��������{cn}��ǰn���Tn.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������C��y2��2px��p��0���Ľ�����F��ֱ��y��2��������C�Ľ��㵽F�ľ������2��
��1����������C�ķ��̣�
��2�����㣨2��0��б��Ϊk��ֱ��l��������C��A��B���㣬OΪ����ԭ�㣬ֱ��AO��ֱ��x����2�ཻ�ڵ�P����֤��BP��x�ᣮ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��Ϊ�������ȵ����У�
��Ϊ�������ȵ����У�![]() Ϊ
Ϊ![]() ��ǰn��ͣ�
��ǰn��ͣ�![]() ��
��
![]() ��
��![]() ����
����![]() ��ֵ��
��ֵ��
![]() ��
��![]() �ǹ���Ϊ
�ǹ���Ϊ![]() �ĵȱ����У���֤������
�ĵȱ����У���֤������![]() Ϊ�ȱ����У�
Ϊ�ȱ����У�
![]() ��
��![]() �ĸ����Ϊ�㣬
�ĸ����Ϊ�㣬![]() �ǹ���Ϊd�ĵȲ����У���֤��
�ǹ���Ϊd�ĵȲ����У���֤��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ɵȲ����еij�Ҫ������
�ɵȲ����еij�Ҫ������![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У��㼯A��{��x��y��|x2+y2��1}��B��{��x��y��|x��4��y��0��3x��4y��0}����㼯Q��{��x��y��|x��x1+x2��y��y1+y2����x1��y1����A����x2��y2����B}����ʾ����������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �ڶ���������������ͬ�ļ�ֵ��.
�ڶ���������������ͬ�ļ�ֵ��.
������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
������![]() ��������ͬ�ļ�ֵ��
��������ͬ�ļ�ֵ��![]() ����
����![]() ��������ʽ
��������ʽ![]() �����������ʵ��
�����������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com