
【题目】已知定义在[0,1]上的函数f(x)满足:
①f(0)=f(1)=0;
②对所有x,y∈[0,1],且x≠y,有|f(x)﹣f(y)|< ![]() |x﹣y|.
|x﹣y|.
若对所有x,y∈[0,1],|f(x)﹣f(y)|<m恒成立,则m的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:依题意,定义在[0,1]上的函数y=f(x)的斜率|k|< ![]() ,
,
依题意可设k>0,构造函数f(x)= 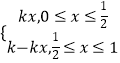 (0<k<
(0<k< ![]() ),满足f(0)=f(1)=0,|f(x)﹣f(y)|<
),满足f(0)=f(1)=0,|f(x)﹣f(y)|< ![]() |x﹣y|.
|x﹣y|.
当x∈[0, ![]() ],且y∈[0,
],且y∈[0, ![]() ]时,|f(x)﹣f(y)|=|kx﹣ky|=k|x﹣y|≤k|
]时,|f(x)﹣f(y)|=|kx﹣ky|=k|x﹣y|≤k| ![]() ﹣0|=k×
﹣0|=k× ![]() <
< ![]() ;
;
当x∈[0, ![]() ],且y∈[
],且y∈[ ![]() ,1],|f(x)﹣f(y)|=|kx﹣(k﹣ky)|=|k(x+y)﹣k|≤|k(1+
,1],|f(x)﹣f(y)|=|kx﹣(k﹣ky)|=|k(x+y)﹣k|≤|k(1+ ![]() )﹣k|=
)﹣k|= ![]() <
< ![]() ;
;
当y∈[0, ![]() ],且x∈[
],且x∈[ ![]() ,1]时,同理可得,|f(x)﹣f(y)|<
,1]时,同理可得,|f(x)﹣f(y)|< ![]() ;
;
当x∈[ ![]() ,1],且y∈[
,1],且y∈[ ![]() ,1]时,|f(x)﹣f(y)|=|(k﹣kx)﹣(k﹣ky)|=k|x﹣y|≤k×(1﹣
,1]时,|f(x)﹣f(y)|=|(k﹣kx)﹣(k﹣ky)|=k|x﹣y|≤k×(1﹣ ![]() )=
)= ![]() <
< ![]() ;
;
综上所述,对所有x,y∈[0,1],|f(x)﹣f(y)|< ![]() ,
,
∵对所有x,y∈[0,1],|f(x)﹣f(y)|<m恒成立,
∴m≥ ![]() ,即m的最小值为
,即m的最小值为 ![]() .
.
故选:B.
【考点精析】根据题目的已知条件,利用绝对值不等式的解法的相关知识可以得到问题的答案,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】如图l,在正方形ABCD中,AB=2,E是AB边的中点,F是BC边上的一点,对角线AC分别交DE、DF于M、N两点.将ADAE,CDCF折起,使A、C重合于A点,构成如图2所示的几何体.
(I)求证:A′D⊥面A′EF;
(Ⅱ)试探究:在图1中,F在什么位置时,能使折起后的几何体中EF∥平面AMN,并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是中国古代第一部数学专著,成于公元一世纪左右,系统总结了战国、秦、汉时期的数学成就.其中《方田》一章中记载了计算弧田(弧田就是由圆弧和其所对弦所围成弓形)的面积所用的经验公式:弧田面积=![]() (弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为
(弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为![]() ,弦长为
,弦长为![]() 的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为( )平方米.(其中
的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为( )平方米.(其中![]() ,
,![]() )
)
A. 15 B. 16 C. 17 D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() ,
, ![]() ,
, ![]() 是非零向量,已知命题p:若
是非零向量,已知命题p:若 ![]()
![]() =0,
=0, ![]()
![]() =0,则
=0,则 ![]()
![]() =0;命题q:若
=0;命题q:若 ![]() ∥
∥ ![]() ,
, ![]() ∥
∥ ![]() ,则
,则 ![]() ∥
∥ ![]() ,则下列命题中真命题是( )
,则下列命题中真命题是( )
A.p∨q
B.p∧q
C.(¬p)∧(¬q)
D.p∨(¬q)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=3sin(2x+ ![]() )的图象向右平移
)的图象向右平移 ![]() 个单位长度,所得图象对应的函数( )
个单位长度,所得图象对应的函数( )
A.在区间[ ![]() ,
, ![]() ]上单调递减
]上单调递减
B.在区间[ ![]() ,
, ![]() ]上单调递增
]上单调递增
C.在区间[﹣ ![]() ,
, ![]() ]上单调递减
]上单调递减
D.在区间[﹣ ![]() ,
, ![]() ]上单调递增
]上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
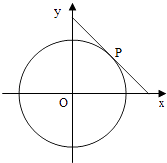
【题目】圆x2+y2=4的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图),双曲线C1: ![]() 过点P且离心率为
过点P且离心率为 ![]() .
. 
(1)求C1的方程;
(2)若椭圆C2过点P且与C1有相同的焦点,直线l过C2的右焦点且与C2交于A,B两点,若以线段AB为直径的圆过点P,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级共有学生![]() 名,为了解学生某次月考的情况,抽取了部分学生的成绩(得分均为整数,满分为
名,为了解学生某次月考的情况,抽取了部分学生的成绩(得分均为整数,满分为![]() 分)进行统计,绘制出如下尚未完成的频率分布表:
分)进行统计,绘制出如下尚未完成的频率分布表:
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
|
| |
| ||
|
|
(1)补充完整题中的频率分布表;
(2)若成绩在![]() 为优秀,估计该校高三年级学生在这次月考中,成绩优秀的学生约为多少人.
为优秀,估计该校高三年级学生在这次月考中,成绩优秀的学生约为多少人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,公路AM,AN围成一块顶角为α的角形耕地,其中tanα=-2,在该块土地中P处有一小型建筑,经测量,它到公路AM,AN的距离分别为3km,![]() km,现要过点P修建一条直线公路BC,将三条公路围成的区域ABC建成一个工业园,为尽量减少耕地占用,问如何确定B点的位置,使得该工业园区的面积最小?并求最小面积.
km,现要过点P修建一条直线公路BC,将三条公路围成的区域ABC建成一个工业园,为尽量减少耕地占用,问如何确定B点的位置,使得该工业园区的面积最小?并求最小面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com