
【题目】某省高考改革新方案,不分文理科,高考成绩实行“3+3”的构成模式,第一个“3”是语文、数学、外语,每门满分150分,第二个“3”由考生在思想政治、历史、地理、物理、化学、生物6个科目中自主选择其中3个科目参加等级性考试,每门满分100分,高考录取成绩卷面总分满分750分.为了调查学生对物理、化学、生物的选考情况,将“某市某一届学生在物理、化学、生物三个科目中至少选考一科的学生”记作学生群体S,从学生群体S中随机抽取了50名学生进行调查,他们选考物理,化学,生物的科目数及人数统计如表:
选考物理、化学、生物的科目数 | 1 | 2 | 3 |
人数 | 5 | 25 | 20 |
(I)从所调查的50名学生中任选2名,求他们选考物理、化学、生物科目数量不相等的概率;
(II)从所调查的50名学生中任选2名,记X表示这2名学生选考物理、化学、生物的科目数量之差的绝对值,求随机变量X的分布列和数学期望;
(III)将频率视为概率,现从学生群体S中随机抽取4名学生,记其中恰好选考物理、化学、生物中的两科目的学生数记作Y,求事件“y≥2”的概率.
【答案】解:(Ⅰ)记“所选取的2名学生选考物理、化学、生物科目数量相等”为事件A,
则 ![]() ,
,
所以他们选考物理、化学、生物科目数量不相等的概率为
![]() ;
;
(Ⅱ)由题意可知X的可能取值分别为0,1,2;
则. ![]() ,
,
![]() ,
,
![]() ;
;
从而X的分布列为:
X | 0 | 1 | 2 |
p | | | |
数学期望为 ![]() ;
;
(Ⅲ)所调查的50名学生中物理、化学、生物选考两科目的学生有25名,
相应的频率为 ![]() ,
,
由题意知,Y~ ![]() ;
;
所以事件“Y≥2”的概率为
![]() .
.
【解析】(Ⅰ)计算“所选取的2名学生选考物理、化学、生物科目数量相等”为事件A,利用对立事件的概率公式计算选考物理、化学、生物科目数量不相等的概率值;(Ⅱ)由题意知X的可能取值,计算对应的概率值,写出X的分布列,计算数学期望值;(Ⅲ)计算所调查的50名学生中物理、化学、生物选考两科目的学生人数,求出相应的频率,根据n次独立重复实验恰有k次发生的概率,求出对应的概率值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C1 , 抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点O,从每条曲线上各取两个点,其坐标分别是(3,一2 ![]() ),(一2,0),(4,一4),(
),(一2,0),(4,一4),( ![]() ). (Ⅰ)求C1 , C2的标准方程;
). (Ⅰ)求C1 , C2的标准方程;
(Ⅱ)是否存在直线L满足条件:①过C2的焦点F;②与C1交与不同的两点M,N且满足 ![]() ?若存在,求出直线方程;若不存在,说明理由.
?若存在,求出直线方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中为了解高中学生的性别和喜欢打篮球是否有关,对50名高中学生进行了问卷调查,得到如下列联表:
喜欢打篮球 | 不喜欢打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 |
已知在这50人中随机抽取1人,抽到喜欢打篮球的学生的概率为 ![]()
(Ⅰ)请将上述列联表补充完整;
(Ⅱ)判断是否有99.5%的把握认为喜欢打篮球与性别有关?
附:K2= ![]()
p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点M(2,2),N(5,-2),点P在x轴上,分别求满足下列条件的点P的坐标.
(1)∠MOP=∠OPN(O是坐标原点).
(2)∠MPN是直角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 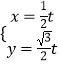 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 ![]() (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为(2
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为(2 ![]() ,
, ![]() ). (Ⅰ)求直线l以及曲线C的极坐标方程;
). (Ⅰ)求直线l以及曲线C的极坐标方程;
(Ⅱ)设直线l与曲线C交于A,B两点,求△PAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知棱长为1的正方体ABCD-A1B1C1D1中,点E,F,M分别是AB,AD,AA1的中点,又P,Q分别在线段A1B1,A1D1上,且A1P=A1Q=x,0<x<1,设平面MEF∩平面MPQ=l,则下列结论中不成立的是 ( )
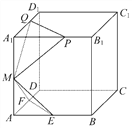
A. l∥平面ABCD
B. l⊥AC
C. 平面MEF与平面MPQ不垂直
D. 当x变化时,l不是定直线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校大一新生中的6名同学打算参加学校组织的“演讲团”、“吉他协会”等五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中没有人参加“演讲团”的不同参加方法数为( )
A.3600
B.1080
C.1440
D.2520
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知正方体ABCD-A1B1C1D1.
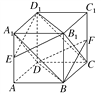
(1)求证:平面A1BD∥平面B1D1C.
(2)若E,F分别是AA1,CC1的中点,求证:平面EB1D1∥平面FBD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】节日前夕,小李在家门前的树上挂了两串彩灯,这两串彩灯的第一次闪亮相互独立,且都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以4秒为间隔闪亮,那么这两串彩灯同时通电后,它们第一次闪亮的时候相差不超过2秒的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com