练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数对任意实数，恒有，且当，，又.

    （1）判断的奇偶性；

    （2）求在区间上的最大值；

    （3）是否存在实数，使得不等式对一切都成立？若存在求出；若不存在，请说明理由.

    【答案】（1）奇函数；（2）6；（3）存在，

    【解析】

    （1）先求得，然后求得，由此判断出为奇函数.

    （2）判断出的单调性，由此求得在区间上的最大值.

    （3）根据的单调性和奇偶性化简不等式，根据一元二次不等式恒成立的条件列不等式，解不等式求得的取值范围.

    （1）依题意，函数对任意实数，恒有.

    令，得，解得.

    令，得，即，故函数为奇函数.

    （2）任取，即，即，所以在上递减.所以在区间上的最大值为.

    （3）由（1）（2）知是在上递减的奇函数，故由得，即，即，对对一切都成立，所以，即，解得.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某厂生产的产品在出厂前都要做质量检测，每一件一等品都能通过检测，每一件二等品通过检测的概率为.现有10件产品，其中6件是一等品，4件是二等品.

    (Ⅰ) 随机选取1件产品，求能够通过检测的概率；

    (Ⅱ)随机选取3件产品，其中一等品的件数记为，求的分布列；

    (Ⅲ)随机选取3件产品，求这三件产品都不能通过检测的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 .

    (1)当时，求曲线在点处的切线方程；

    (2)当时，设函数，且函数有且仅有一个零点，若当时， 恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】今年的西部决赛勇士和火箭共进行了七场比赛，经历了残酷的“抢七”比赛，两队的当家球星库里和杜兰特七场比赛的每场比赛的得分如下表：

    第一场

    第二场

    第三场

    第四场

    第五场

    第六场

    第七场

    库里

    26

    28

    24

    22

    31

    29

    36

    杜兰特

    26

    29

    33

    26

    40

    29

    27

    （1）绘制两人得分的茎叶图；

    （2）分析并比较两位球星的七场比赛的平均得分及得分的稳定程度.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f(x)＝x3－6x＋5，x∈R.

    (1)求函数f(x)的极值；(2)若关于x的方程f(x)＝a有三个不同的实根，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图是某手机商城2018年华为、苹果、三星三种品牌的手机各季度销量的百分比堆积图（如：第三季度华为销量约占50%，苹果销量约占20%，三星销量约占30%）．根据该图，以下结论中一定正确的是（　　）

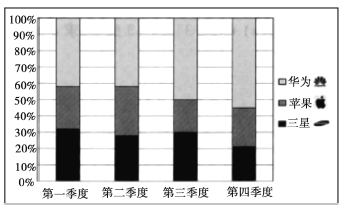
    A.华为的全年销量最大B.苹果第二季度的销量大于第三季度的销量

    C.华为销量最大的是第四季度D.三星销量最小的是第四季度

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解春季昼夜温差大小与某种子发芽多少之间的关系，现在从4月份的30天中随机挑选了5天进行研究，且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数，得到如下表格：

    日期

    4月1日

    4月7日

    4月15日

    4月21日

    4月30日

    温差x/℃

    10

    11

    13

    12

    8

    发芽数y/颗

    23

    25

    30

    26

    16

    （1）从这5天中任选2天,记发芽的种子数分别为,求事件“均不小于25”的概率；

    （2） 若由线性回归方程得到的估计数据与4月份所选5天的检验数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的. 请根据4月7日，4月15日与4月21日这三天的数据，求出关于的线性回归方程，并判定所得的线性回归方程是否可靠？

    参考公式: ，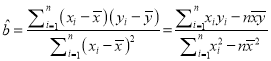

    参考数据:

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着支付宝、微信等支付方式的上线，越来越多的商业场景可以实现手机支付.为了解各年龄层的人使用手机支付的情况，随机调查了50个人，并把调查结果制成下表：

    （1）把年龄在称为中青年，年龄在称为中老年，请根据上表完成列联表，是否有以上的把握判断使用手机支付与年龄（中青年、中老年）有关联？

    （2）若分别从年龄在、的被调查者中各随机选取2人进行调查，记选中的4人中使用手机支付的人数记为，求.

    附：可能用到的公式：，其中

    0.100

    0.050

    0.025

    0.010

    0.005

    2.706

    3.841

    5.024

    6.635

    7.879

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系，将曲线上的每一个点的横坐标保持不变，纵坐标缩短为原来的，得到曲线，以坐标原点为极点， 轴的正半轴为极轴，建立极坐标系， 的极坐标方程为．

    （Ⅰ）求曲线的参数方程；

    （Ⅱ）过原点且关于轴对称的两条直线与分别交曲线于、和、，且点在第一象限，当四边形的周长最大时，求直线的普通方程．

    查看答案和解析>>

    同步练习册答案