练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．将5名应届大学毕业生分给3个用人单位，每个单位至少1名，一共有150种分配方案．（用数字作答）

    分析 根据题意，则分2步进行分析：①5名应届大学毕业生，分为3组，②将3组进行全排列对应3个用人单位即可；分别求出每一步的情况数目，由分步计数原理计算可得答案．

    解答 解：根据题意，5名应届大学毕业生，可以分组为（3，1，1），（2，2，1），
    其分组的种数为C53+C51C42÷2=25，
    再分配给3个用人单位，由分步原理得，共有25•A33=150种分法．
    故答案为：150．

    点评 本题考查排列、组合的运用，此类问题一般是先分组，再分配，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    6．秦九韶是我国南宋时期的数学家，他在所著的《数学九章》中提出多项式求值的秦九韶算法，如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例，依次输入a为2，2，5，则输出的s=（　　）
    A．7B．12C．17D．34

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知圆O的半径为R（R为常数），它的内接三角形ABC满足2R（sin2A-sin2C）=（a-b）sinB，其中a，b，c分别为角A，B，C的对边．
    （1）求角C；
    （2）若c=$\sqrt{7}$，且△ABC的面积为$\frac{{3\sqrt{3}}}{2}$，求△ABC的周长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．设z∈C，且（1-i）z=2i（i是虚数单位），则|z|=$\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知直线l：Ax+By+C=0（A、B不全为零）与圆x2+y2=1交于M、N两点，且|MN|=$\sqrt{3}$，若O为坐标原点，则$\overrightarrow{OM}$•$\overrightarrow{ON}$的值为-$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．一轮船行驶时，单位时间的燃料费u与其速度v的立方成正比，若轮船的速度为每小时20km时，燃料费为每小时40元，其余费用每小时为270元，这部分费用不随速度而变化．
    （1）求u是v的函数关系式；
    （2）求轮船速度为多少时，轮船航行每千米的费用最少（轮船最高速度为bkm/小时）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知α是第三象限角，化简f（x）=$\frac{sin（α-\frac{π}{2}）cos（\frac{3}{2}π+α）tan（π-α）}{tan（-α-π）sin（-π-α）}$=-cosα．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．如图，在平面直角坐标系xOy中，以Ox轴为始边做锐角α和钝角β，它们的终边分别与单位圆相交于A、B两点，已知A、B的纵坐标分别为$\frac{{\sqrt{5}}}{5}$，$\frac{{\sqrt{10}}}{10}$．
    （1）求tan（2α-β）的值； 
    （2）求β-α的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

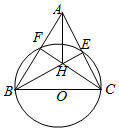    12．如图，△ABC中，以BC为直径的⊙O分别交AC，AB于点E，F，BE，CF交于点H．求证：
    （Ⅰ）过C点平行于AH的直线是⊙O的切线；
    （Ⅱ）BH•BE+CH•CF=BC2．

    查看答案和解析>>

    同步练习册答案