
【题目】当n为正整数时,函数N(n)表示n的最大奇因数,如N(3)=3,N(10)=5,…,设Sn=N(1)+N(2)+N(3)+N(4)+…+N(2n﹣1)+N(2n),则Sn= .
【答案】![]()
【解析】解:由N(x)的性质可得知,当x是奇数时,x的最大奇数因子明显是它本身.因此N(x)=x,当x是偶数时,参看下面的讨论, 因此由这样一个性质,我们就可将Sn进行分解,分别算出奇数项的和与偶数项的和进而相加,即Sn=S奇+S偶 ,
∴S奇=N(1)+N(3)+…+N(2n﹣1)=1+3+…2n﹣1= ![]() =4n﹣1
=4n﹣1
当x是偶数时,且x∈[2k , 2k+1)①当k=1时,x∈[2,4)该区间包含的偶数只有2,而N(2)=1所以该区间所有的偶数的最大奇因数之和为T1=1
②当k=2时,x∈[4,8),该区间包含的偶数为4,6,所以该区间所有的最大奇因数偶数之和为T2=1+3=4
③当k=3时,x∈[8,16),该区间包含的偶数为8,10,12,14,则该区间所有偶数的最大奇因数之和为T3=1+3+5+7=16,因此我们可以用数学归纳法得出当x∈[2k , 2k+1)该区间所有偶数的最大奇因数和Tk=4k﹣1 .
∴对k从1到n﹣1求和得T1+T2+…+Tn﹣1= ![]()
∴S偶=T1+T2+…+Tn﹣1+N(2n)= ![]()
综上可知Sn=S奇+S偶=4n﹣1+ ![]() =
= ![]()
所以答案是 ![]()
【考点精析】通过灵活运用数列的前n项和,掌握数列{an}的前n项和sn与通项an的关系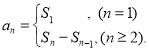 即可以解答此题.
即可以解答此题.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP= ![]() .
.
(Ⅰ)求证:AB⊥PC;
(Ⅱ)求点D到平面PAC的距离.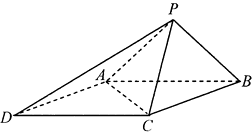
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在以下关于向量的命题中,不正确的是( )
A.若向量 ![]() ,向量
,向量 ![]() (xy≠0),则
(xy≠0),则 ![]()
B.若四边形ABCD为菱形,则 ![]()
C.点G是△ABC的重心,则 ![]()
D.△ABC中, ![]() 和
和 ![]() 的夹角等于A
的夹角等于A
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知圆C的方程:x2+y2﹣2x﹣4y+4=0,点P是直线l:x﹣2y﹣2=0上的任意点,过P作圆的两条切线PA,PB,切点为A、B,当∠APB取最大值时.
(Ⅰ)求点P的坐标及过点P的切线方程;
(Ⅱ)在△APB的外接圆上是否存在这样的点Q,使|OQ|= ![]() (O为坐标原点),如果存在,求出Q点的坐标,如果不存在,请说明理由.
(O为坐标原点),如果存在,求出Q点的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,且BC=2AD,AD⊥CD,PB⊥CD,点E在棱PD上,且PE=2ED. 
(1)求证:平面PCD⊥平面PBC;
(2)求证:PB∥平面AEC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为D的函数y=f(x),如果存在区间[m,n]D,同时满足: ①f(x)在[m,n]内是单调函数;
②当定义域是[m,n]时,f(x)的值域也是[m,n].
则称[m,n]是该函数的“和谐区间”.
(1)证明:[0,1]是函数y=f(x)=x2的一个“和谐区间”.
(2)求证:函数 ![]() 不存在“和谐区间”.
不存在“和谐区间”.
(3)已知:函数 ![]() (a∈R,a≠0)有“和谐区间”[m,n],当a变化时,求出n﹣m的最大值.
(a∈R,a≠0)有“和谐区间”[m,n],当a变化时,求出n﹣m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
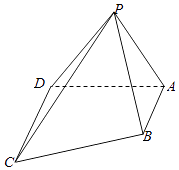
【题目】如图,在四棱锥P﹣ABCD中, ![]() 平面PCD,平面PAD平面ABCD,CD⊥AD,△APD为等腰直角三角形,
平面PCD,平面PAD平面ABCD,CD⊥AD,△APD为等腰直角三角形, ![]() .
. 
(1)证明:平面PAB⊥平面PCD;
(2)若三棱锥B﹣PAD的体积为 ![]() ,求平面PAD与平面PBC所成二面角的余弦值.
,求平面PAD与平面PBC所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计算下列几个式子,结果为 ![]() 的序号是 . ①tan25°+tan35°
的序号是 . ①tan25°+tan35° ![]() tan25°tan35°,
tan25°tan35°,
② ![]() ,
,
③2(sin35°cos25°+sin55°cos65°),
④ ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com