
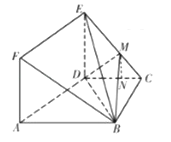
【题目】如图,边长为![]() 的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,DC=BC=
的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,DC=BC=![]() AB=1,点M在线段EC上.
AB=1,点M在线段EC上.
(Ⅰ)证明:平面BDM⊥平面ADEF;
(Ⅱ)判断点M的位置,使得三棱锥B﹣CDM的体积为![]() .
.

【答案】(Ⅰ)见解析;(Ⅱ)点M在线段CE的三等分点且靠近C处.
【解析】试题分析:
(Ⅰ)由题意结合勾股定理可得AD⊥BD,由面面垂直的性质可得BD⊥ED,据此可得BD⊥平面ADEF,故平面BDM⊥平面ADEF;
(Ⅱ)在平面DMC内,过M作MN⊥DC,垂足为N,转换顶点,VB﹣CDM=VM﹣CDB,据此可得![]() ,利用相似三角形的性质可得
,利用相似三角形的性质可得![]() ,即点M在线段CE的三等分点且靠近C处.
,即点M在线段CE的三等分点且靠近C处.
试题解析:
(Ⅰ)∵DC=BC=1,DC⊥BC,
∴BD=![]() ,
,
∵AD=![]() ,AB=2,
,AB=2,
∴AD2+BD2=AB2 ,
∴∠ADB=90°,
∴AD⊥BD,
∵平面ADEF⊥平面ABCD,ED⊥AD,平面ADEF∩平面ABCD=AD,
∴ED⊥平面ABCD,
∴BD⊥ED,
∵AD∩DE=D,
∴BD⊥平面ADEF,
∵BD平面BDM,
∴平面BDM⊥平面ADEF;
(Ⅱ)如图,在平面DMC内,过M作MN⊥DC,垂足为N,则MN∥ED,
∵ED⊥平面ABCD,
∴MN⊥平面ABCD,
∵VB﹣CDM=VM﹣CDB=![]() ,
,
∴![]() ×
×![]() ×1×1×MN=
×1×1×MN=![]() ,
,
∴MN=![]() ,
,
∴![]() =
=![]() ,
,
∴CM=![]() CE,
CE,
∴点M在线段CE的三等分点且靠近C处.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某校夏令营有3名男同学![]() 和3名女同学
和3名女同学![]() ,其年级情况如下表,现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同).
,其年级情况如下表,现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同).
一年级 | 二年级 | 三年级 | |
男同学 |
|
|
|
女同学 |
|
|
|
(1)用表中字母列举出所有可能的结果;
(2)设![]() 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件
为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地小吃“全羊汤”2008年被中国中医学会营养膳食协会评为“中华名吃”,2010年12月被纳入市级非物质文化遗产名录,打造地方名片.当初向各地作广告推广,对销售收益产生额积极的影响.某年度在若干地区各投入4万元广告费用后,将各地该年度的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.

(1)根据频率分布直方图,计算图中各小长方形的宽度;
(2)根据频率分布直方图,估计投入4万元广告费用之后,销售收益的平均值;(以各组区间中点值代表改组的取值)
(3)又在某一地区测的另外一些数据,并整理的得到下表:
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 2 | 7 |
请将(2)的结果填入空白栏,表中的数据![]() 之间存在线性相关关系.计算
之间存在线性相关关系.计算![]() ,并预测年度广告约投入多少万元时,年销售收益达到千万元?(结果精确达到0.1)
,并预测年度广告约投入多少万元时,年销售收益达到千万元?(结果精确达到0.1)
参考公式: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小萌大学毕业后,家里给了她10万元,她想办一个“萌萌”加工厂,根据市场调研,她得出了一组毛利润![]() (单位:万元)与投入成本
(单位:万元)与投入成本![]() (单位:万元)的数据如下:
(单位:万元)的数据如下:
投入成本 | 0.5 | 1 | 2 | 3 | 4 | 5 | 6 |
毛利润 | 1.06 | 1.25 | 2 | 3.25 | 5 | 7.25 | 9.98 |
为了预测不同投入成本情况下的利润,她想在两个模型![]() ,
,![]() 中选一个进行预测.
中选一个进行预测.
(1)根据投入成本2万元和4万元的两组数据分别求出两个模型的函数解析式,请你根据给定数据选出一个较好的函数模型进行预测(不必说明理由),并预测她投入8万元时的毛利润;
(2)若小萌准备最少投入2万元开办加工厂,请预测加工厂毛利润率![]() 的最大值,并说明理由.(
的最大值,并说明理由.(![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“海之旅”表演队在一海滨区域进行集训,该海滨区域的海浪高度![]() (米)随着时刻
(米)随着时刻![]() 而周期性变化.为了了解变化规律,该团队观察若干天后,得到每天各时刻
而周期性变化.为了了解变化规律,该团队观察若干天后,得到每天各时刻![]() 的浪高数据的平均值如下表:
的浪高数据的平均值如下表:
| 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| 1.0 | 1.4 | 1.0 | 0.6 | 1.0 | 1.4 | 0.9 | 0.6 | 1.0 |
(1)从![]() 中选择一个合适的函数模型,并求出函数解析式;
中选择一个合适的函数模型,并求出函数解析式;
(2)如果确定当浪高不低于0.8米时才进行训练,试安排白天内恰当的训练时间段.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线y2=2px(p>0)焦点F的直线与抛物线交于A,B两点,作AC,BD垂直抛物线的准线l于C,D,其中O为坐标原点,则下列结论正确的是 . (填序号)
① ![]() ;
;
②存在λ∈R,使得 ![]() 成立;
成立;
③ ![]() =0;
=0;
④准线l上任意一点M,都使得 ![]() >0.
>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣mx(m∈R).
﹣mx(m∈R).
(1)当m=0时,求函数f(x)的零点个数;
(2)当m≥0时,求证:函数f(x)有且只有一个极值点;
(3)当b>a>0时,总有 ![]() >1成立,求实数m的取值范围.
>1成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:如果函数![]() 在定义域内给定区间
在定义域内给定区间![]() 上存在
上存在![]() ,满足
,满足![]() ,则称函数
,则称函数![]() 是
是![]() 上的“平均值函数”,
上的“平均值函数”,![]() 是它的均值点.
是它的均值点.
(1)![]() 是否是
是否是![]() 上的“平均值函数”,如果是请找出它的均值点;如果不是,请说明理由;
上的“平均值函数”,如果是请找出它的均值点;如果不是,请说明理由;
(2)现有函数![]() 是
是![]() 上的平均值函数,则求实数
上的平均值函数,则求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com