
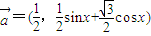 与
与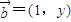 共线,且有函数y=f(x).
共线,且有函数y=f(x). ,边
,边 ,
,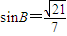 ,求AC的长.
,求AC的长. )=
)=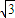 ,根据f(x)的解析式,得到sinA的值,再由sinB及BC的值,利用正弦定理即可求出AC的长.
,根据f(x)的解析式,得到sinA的值,再由sinB及BC的值,利用正弦定理即可求出AC的长. 与
与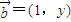 共线,
共线,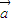 ∥
∥ ,即
,即 y-(
y-( sinx+
sinx+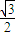 cosx)=0,
cosx)=0, ),
),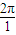 ,
,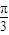 )≤2,
)≤2,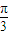 )=
)=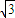 ,得2sin(A-
,得2sin(A-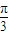 +
+ )=
)=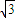 ,即sinA=
,即sinA=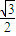 ,
,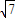 ,sinB=
,sinB=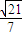 ,
,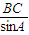 =
=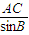 得:AC=
得:AC=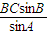 =
= =2.
=2.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
(08年丰台区统一练习一理)(13分)
在平面直角坐标系xOy中,已知点A(-1, 0)、B(1, 0), 动点C满足条件:△ABC的周长为
![]() .记动点C的轨迹为曲线W.
.记动点C的轨迹为曲线W.
(Ⅰ)求W的方程;
(Ⅱ)经过点(0, ![]() )且斜率为k的直线l与曲线W 有两个不同的交点P和Q,
)且斜率为k的直线l与曲线W 有两个不同的交点P和Q,
求k的取值范围;
(Ⅲ)已知点M(![]() ),N(0, 1),在(Ⅱ)的条件下,是否存在常数k,使得向量
),N(0, 1),在(Ⅱ)的条件下,是否存在常数k,使得向量
![]() 与
与![]() 共线?如果存在,求出k的值;如果不存在,请说明理由.
共线?如果存在,求出k的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南灵宝第三高级中学高三上学期第三次质量检测文数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知向量 与
与 共线,且有函数
共线,且有函数
(Ⅰ)求函数 的周期与最大值;
的周期与最大值;
(Ⅱ)已知锐角DABC的三个内角分别是A、B、C,若有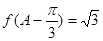 ,边
,边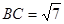 ,
, ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省宁波市鄞州区高三高考适应性3月考试文科数学 题型:解答题
已知向量 与
与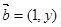 共线,且有函数
共线,且有函数
(Ⅰ)求函数 的周期与最大值;
的周期与最大值;
(Ⅱ)已知锐角DABC的三个内角分别是A、B、C,若有 ,边
,边 ,
, ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:高中数学 来源:浙江省宁波市鄞州区2011-2012学年高三高考适应性考试(3月)数学(文)试题 题型:解答题
已知向量 与
与 共线,且有函数
共线,且有函数
(Ⅰ)求函数 的周期与最大值;
的周期与最大值;
(Ⅱ)已知锐角DABC的三个内角分别是A、B、C,若有 ,边
,边 ,
, ,求AC的长.
,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com